Cube Calculator

Table of Contents

• Cube definition
• Parts of a cube
  • Side length (a)
  • Diagonal (d)
  • Area (A)
  • Volume (V)
  • Inradius (r)
  • Circumradius (R)

Cube definition

A cube is a three-dimensional object with six congruent square faces, twelve straight edges, and eight vertices. It is a regular polyhedron, meaning that it's faces are congruent regular polygons which are assembled in the same way around each vertex.

The cube is also one of the five platonic solids (the other four are: tetrahedron, octahedron, dodecahedron and icosahedron). A Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex.

Parts of a cube

The six parts of a cube mentioned in this tool are side (or edge) length, diagonal, area, volume, inradius and circumradius.

Side length (a)

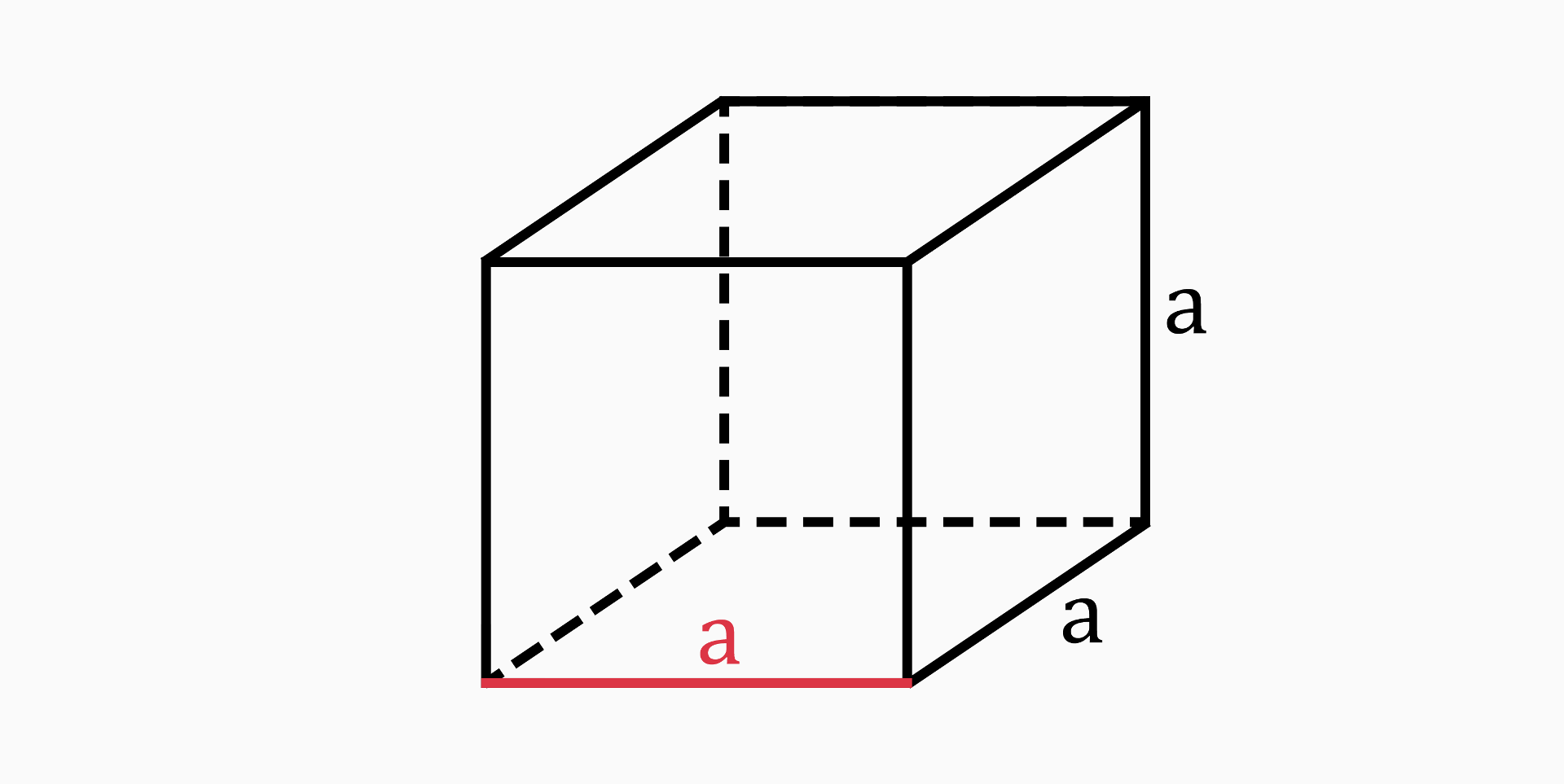
The side length (or edge length) of a cube refers to the length of any one of its edges. In a cube, all six faces are congruent squares, so each edge is of the same length.

The edge length of a cube can be found with the following formulas:

• If you know the volume of the cube:

  a = ³√(V)

• If you know the area:

  a = √(A / 6)

• If you know the diagonal:

  a = d / √(3)

• If you know the inradius:

  a = 2 * r

• If you know the circumradius:

  a = 2 * R / √(3)

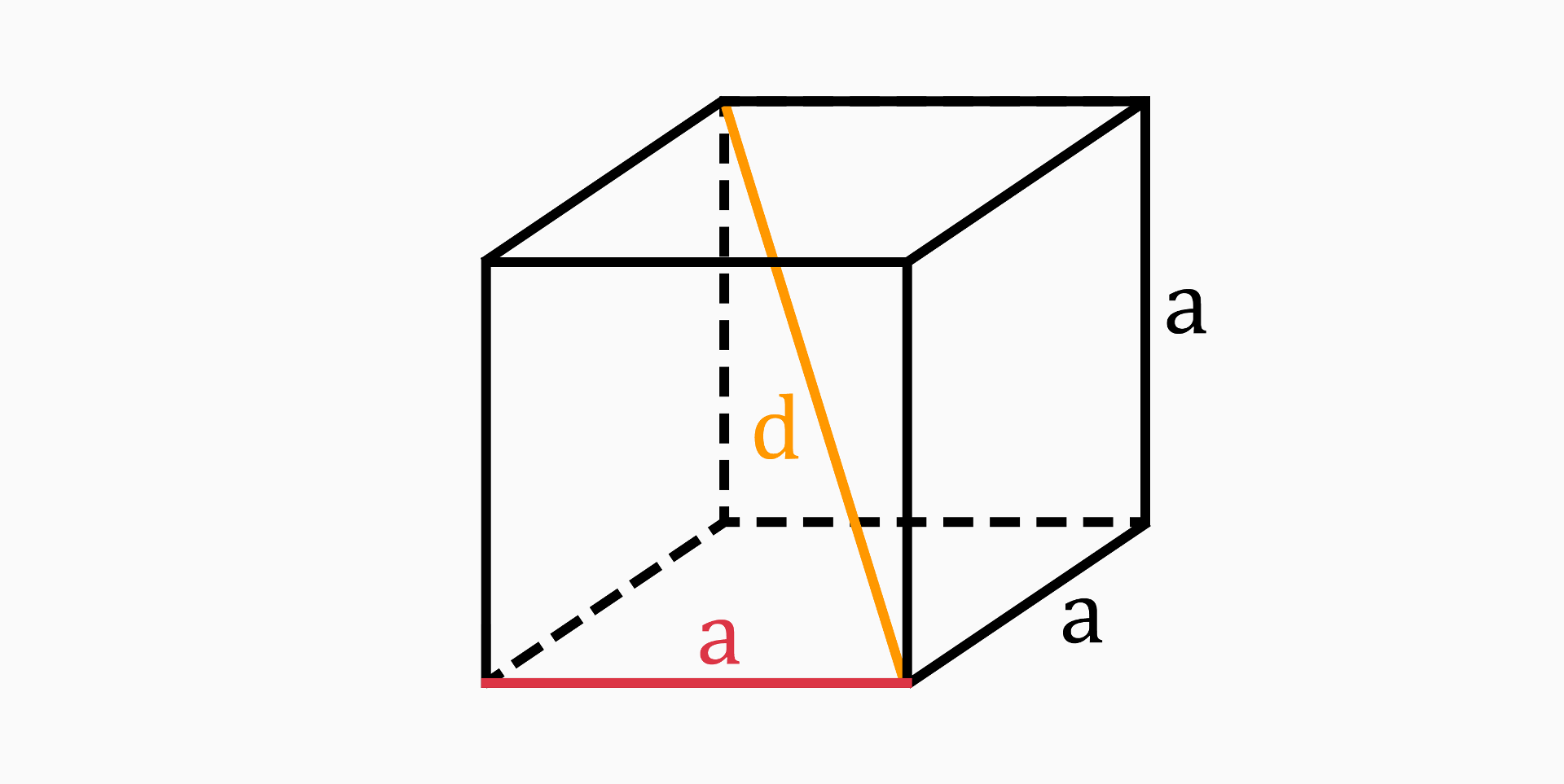
Diagonal (d)

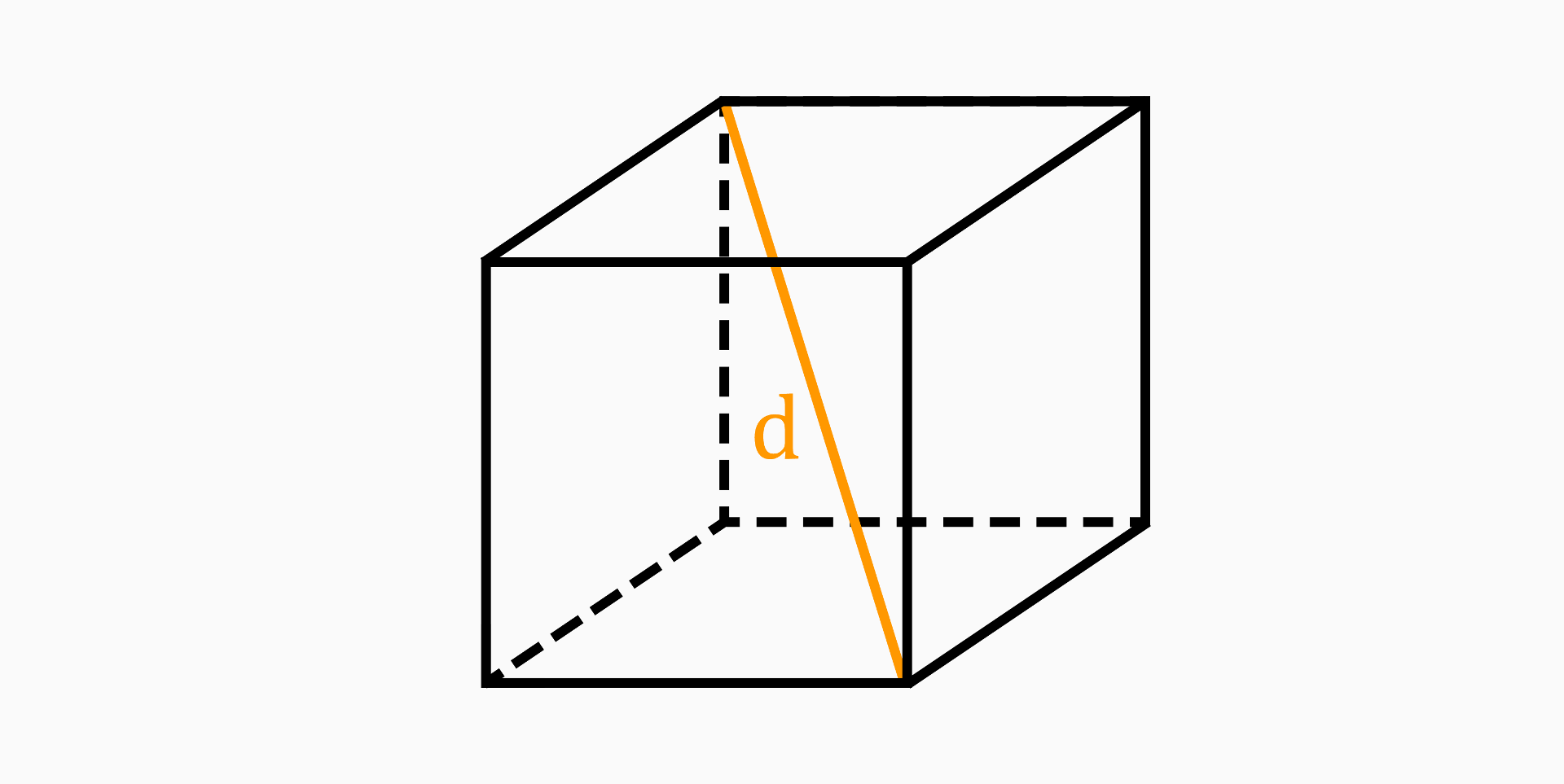
The diagonal of a cube refers to a line segment connecting two opposite vertices of the cube. It is the longest possible line segment that can be drawn inside the cube.

To calculate the diagonal of a cube, you can use the following formula:

d = a * √(3)

Area (A)

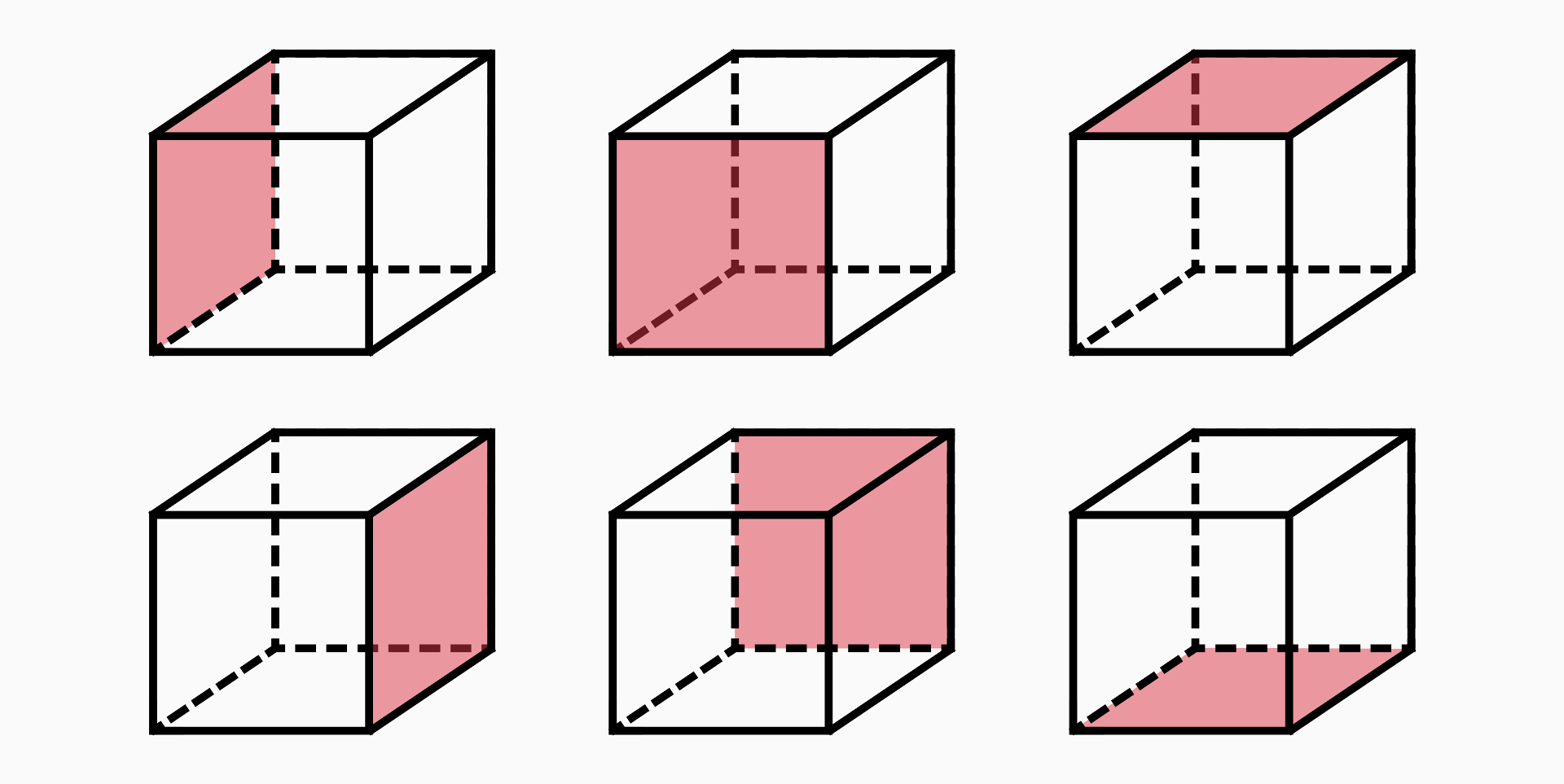
The area of a cube is the sum of the areas of all its faces.

Given that a cube is composed of six equal square faces, the surface area of a cube can be calculated using the formula:

A = 6 * a²

Volume (V)

The volume of a cube is the amount of space contained within the cube.

Because all edges are of equal length, the formula for the volume of a cube is:

V = a³

Inradius (r)

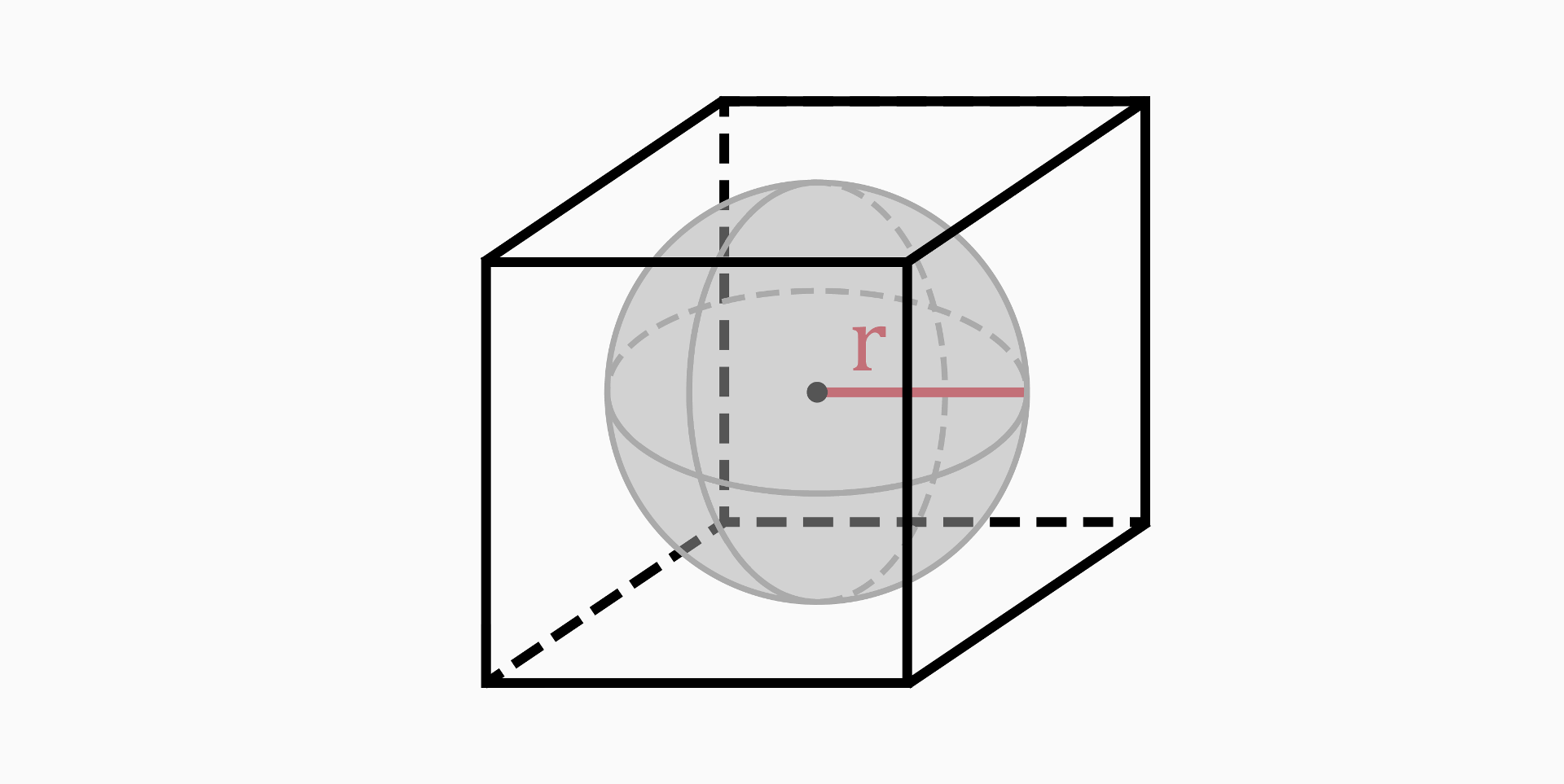
The inradius of a cube is the radius of a sphere that is inscribed within the cube and touches each face of the cube at its center.

The inradius of a cube is equal to half of the edge length:

r = a / 2

Circumradius (R)

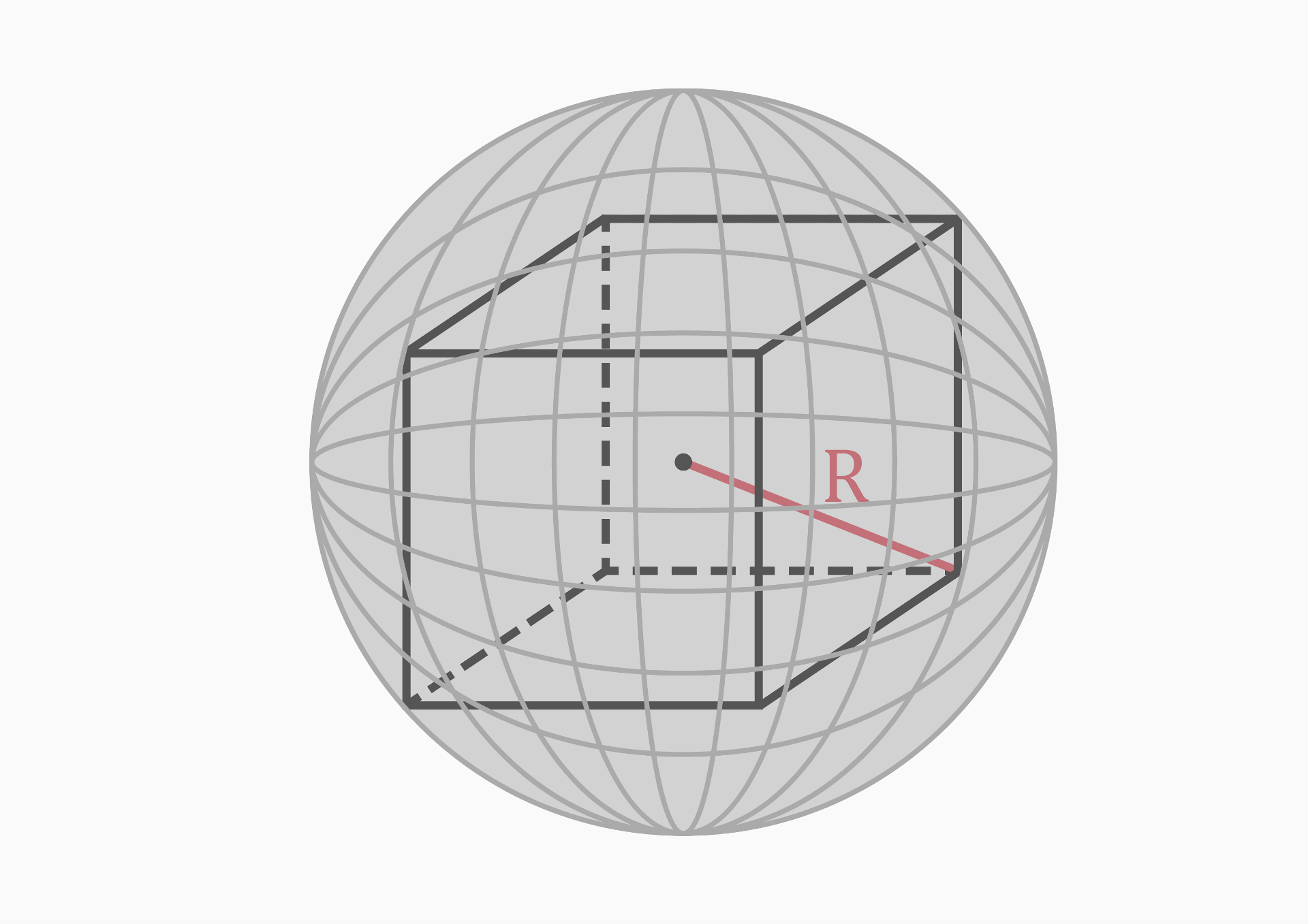
The circumradius of a cube is the radius of a sphere that circumscribes the cube, meaning that it passes through all eight vertices of the cube.

The circumradius of a cube is equal to half the length of its diagonal:

R = d / 2