Square Calculator

Table of Contents

• Square definition
• Parts of a square
  • Side length (a)
  • Area (A)
  • Perimeter (P)
  • Diagonal (d)
  • Inradius (r)
  • Circumradius (R)

Square definition

A square is a regular quadrilateral with four equal sides and four right angles.

It's a special case of a rhombus, a kite, a trapezoid, a parallelogram and a rectangle so it has all properties of these shapes, namely:

• The diagonals bisect each other and meet at 90°.
• The diagonals bisect its angles.
• Opposite sides are both parallel and equal in length.
• All four angles are equal.
• All four sides are equal.
• The diagonals are equal.

Parts of a square

The six parts of a square mentioned in this tool are side length, area, perimeter, diagonal, inradius and circumradius.

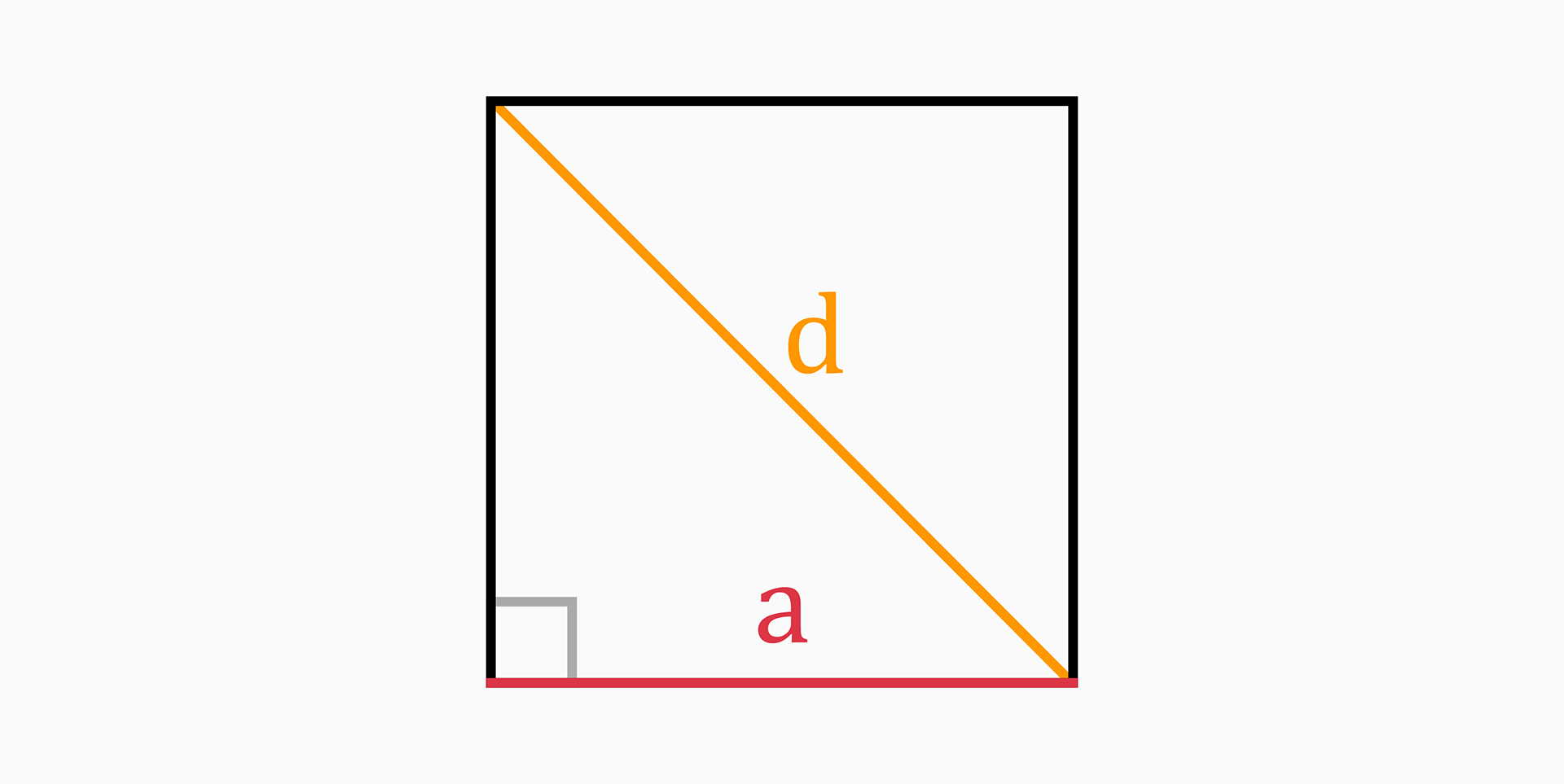
Side length (a)

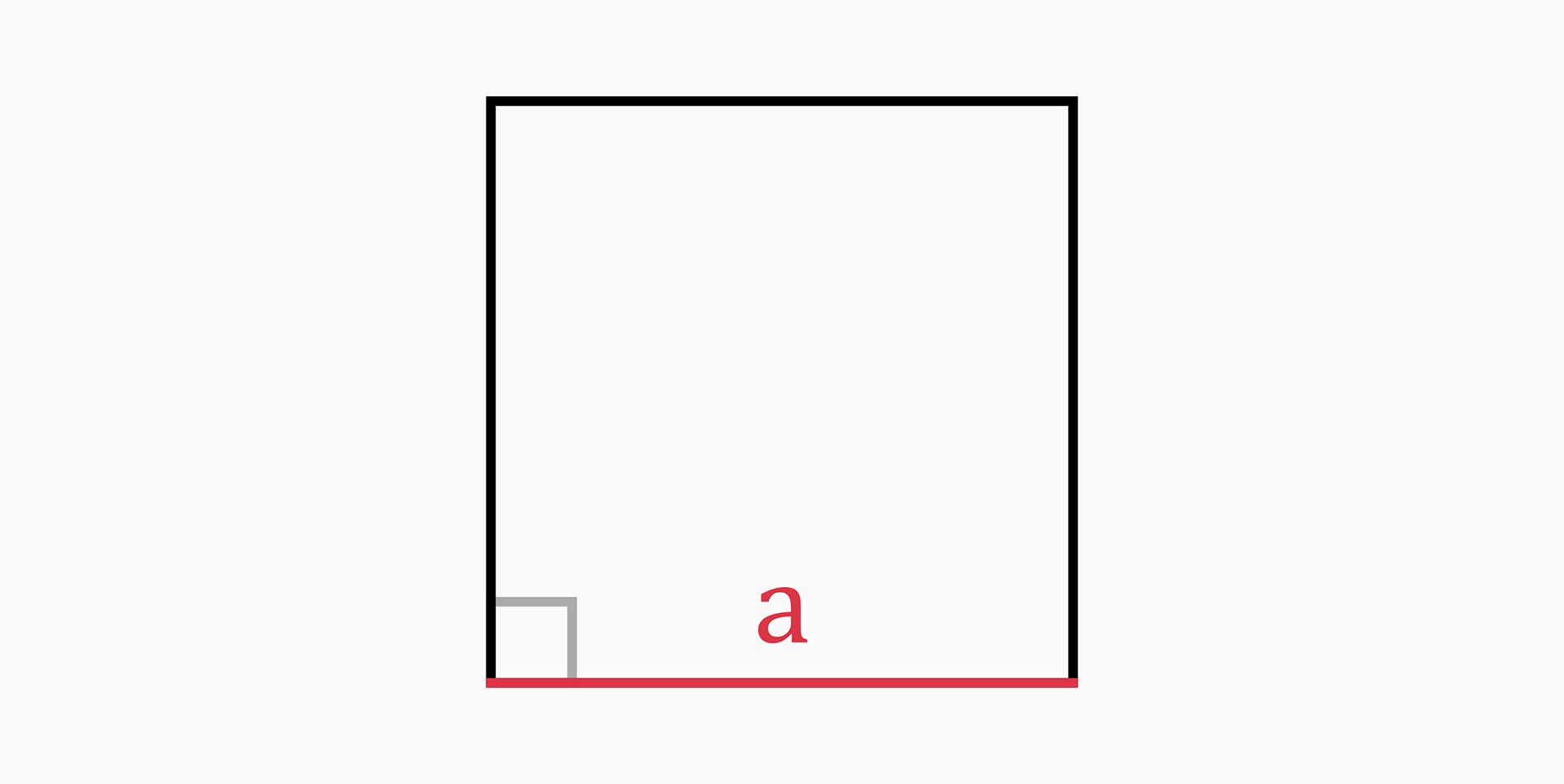
The side length of a square can be found with the following formulas:

• If you know the perimeter of the square:

  a = P / 4

• If you know the area:

  a = √(A)

• If you know the diagonal:

  a = d / √(2)

Area (A)

The area of a square is the region enclosed inside the square.

Since all sides are of the same length, it can be found with the following formula:

A = a²

Perimeter (P)

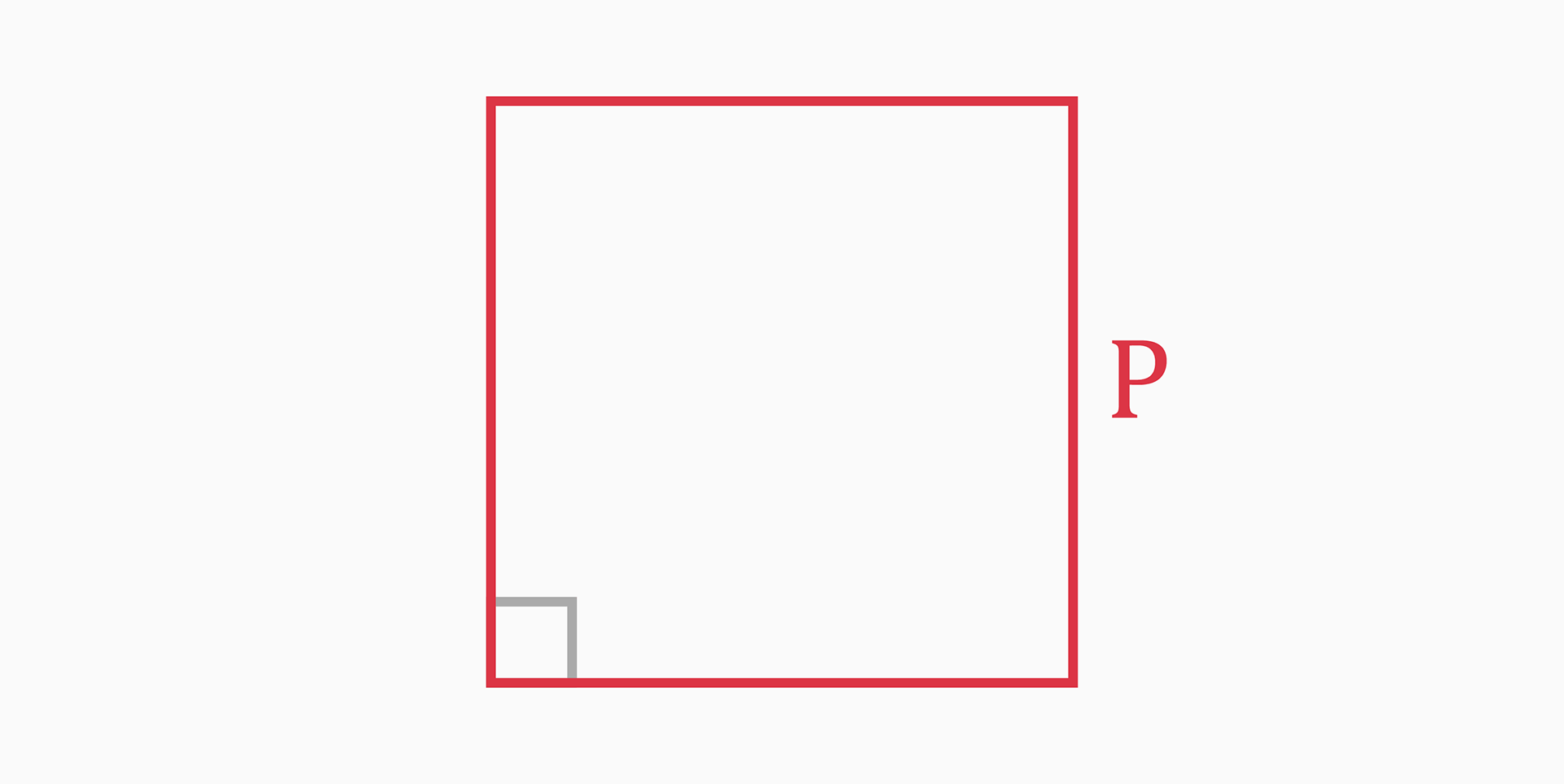
The perimeter of a square is the total length of all sides of the square.

Since all sides are of the same length, it can be found with the following formula:

P = 4 * a

Diagonal (d)

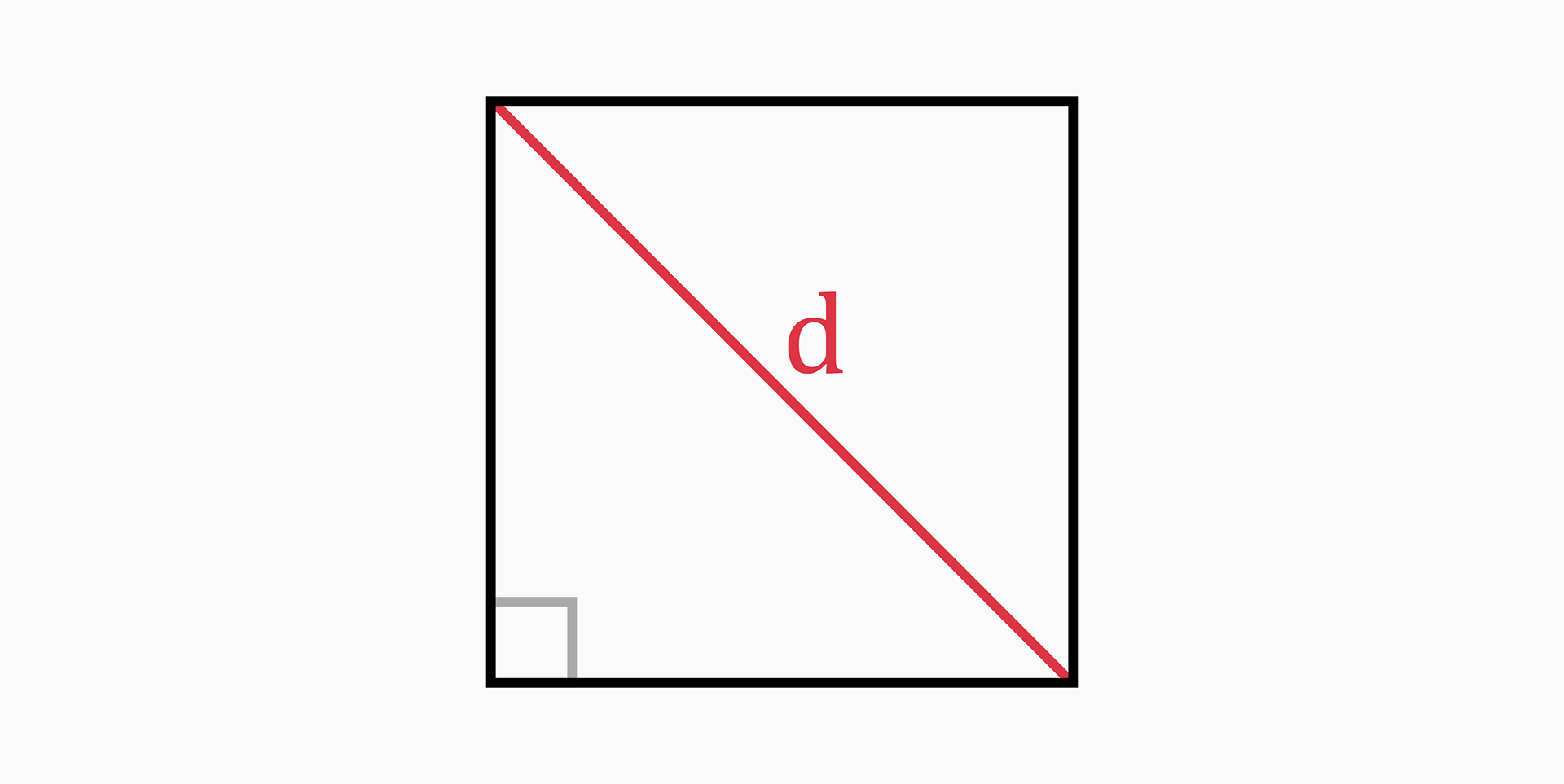
The diagonal is the length of a line stretching from one corner of the square to the opposite corner through the center of the square.

The diagonal of the square cuts the square in two isosceles right triangles; Therefore, we can use the diagonal as the hypotenuse of the triangle.

In this case, the Pythagorean theorem can be applied:

d² = a² + a²

which simplifies to:

d = √(a² + a²)
d = √(2 * a²)
d = a * √(2)

Inradius (r)

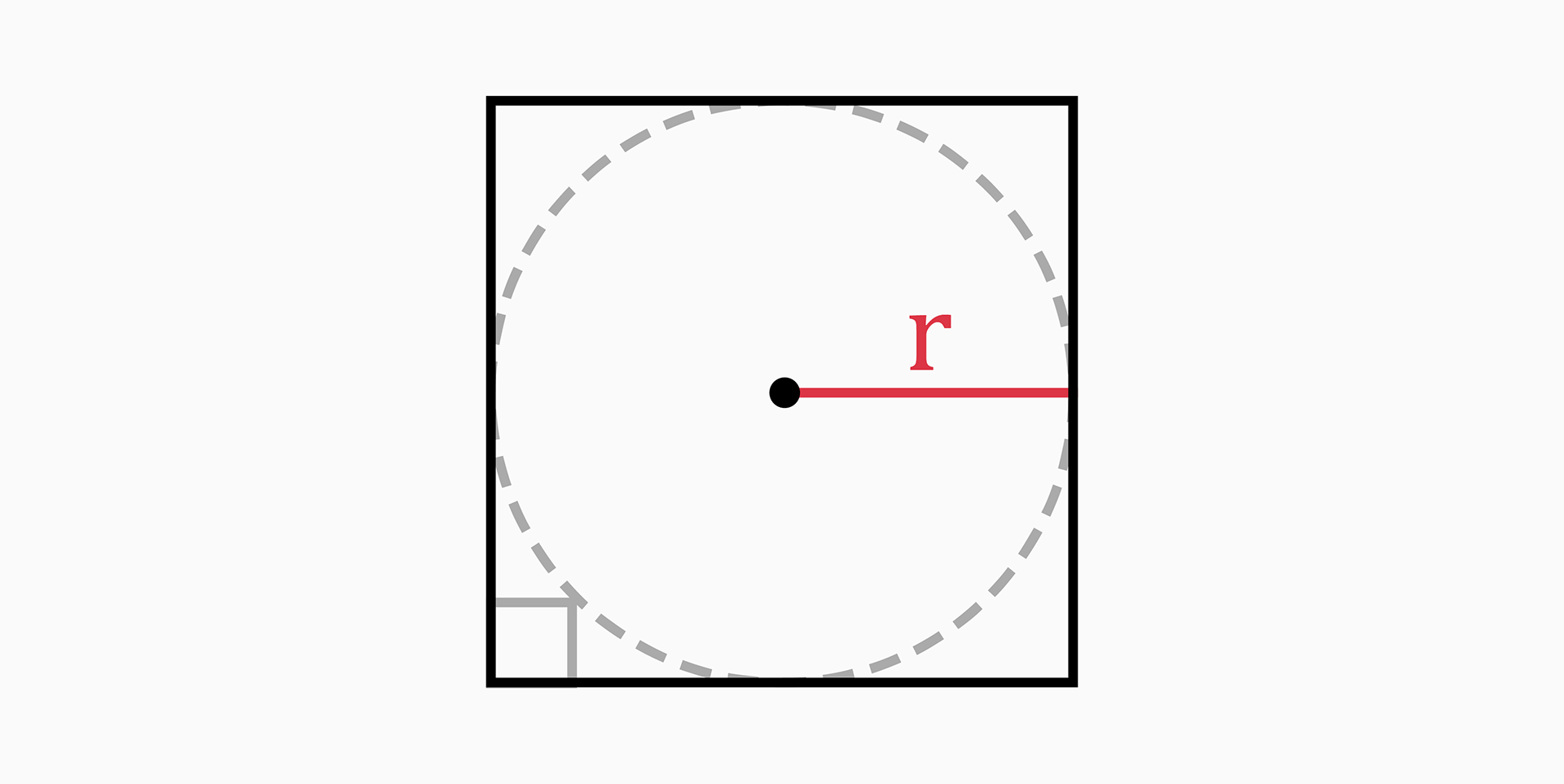
The inradius is the radius of a circle which is drawn inside a square touching all four sides of the square. Therefore, the side length of a square becomes the diameter of the circle.

From the drawing above, we can clearly understand that the inradius is half of the square's side length.

r = a / 2

Circumradius (R)

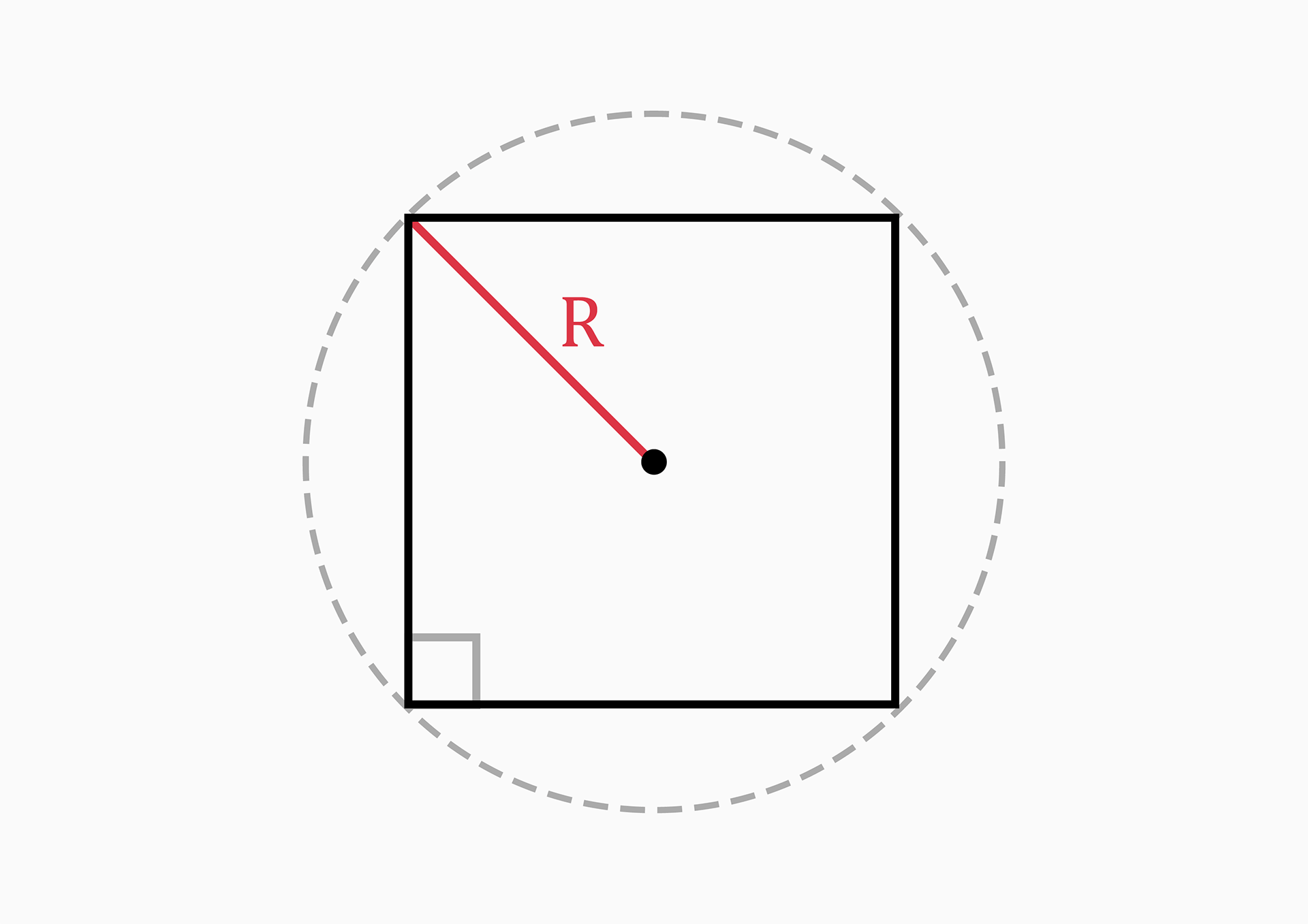
The circumradius is the radius of a circle which is drawn outside a square touching all four vertices (corners) of the square.

From the drawing above, we can see that the circumradius is half of the diagonal of the square.

R = a * √(2) / 2