Rectangle Calculator

Table of Contents

• Rectangle definition
• Parts of a rectangle
  • Length (a)
  • Width (b)
  • Area (A)
  • Perimeter (P)
  • Diagonal (d)
  • Circumradius (R)

Rectangle Definition

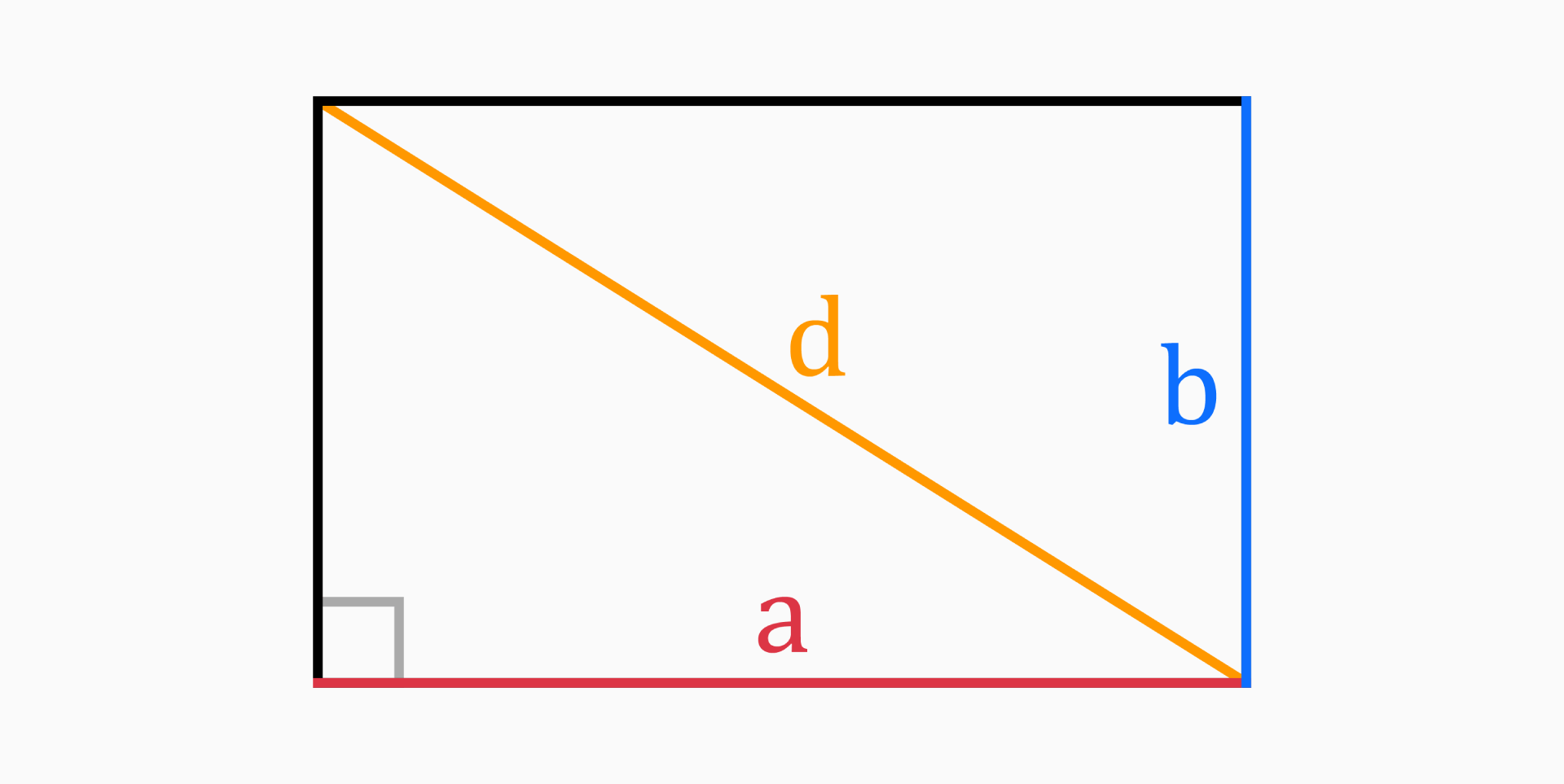
A rectangle is a type of quadrilateral with four straight sides and four right angles, whose opposite sides are equal and parallel.

The word rectangle comes from Latin rectangulus. It's a combination of rectus (which means "right, straight") and angulus (an angle).

Parts of a Rectangle

The six parts of a rectangle mentioned in this tool are length (a), width (b), area (A), perimeter (P), diagonal (d) and circumradius (R).

Length (a)

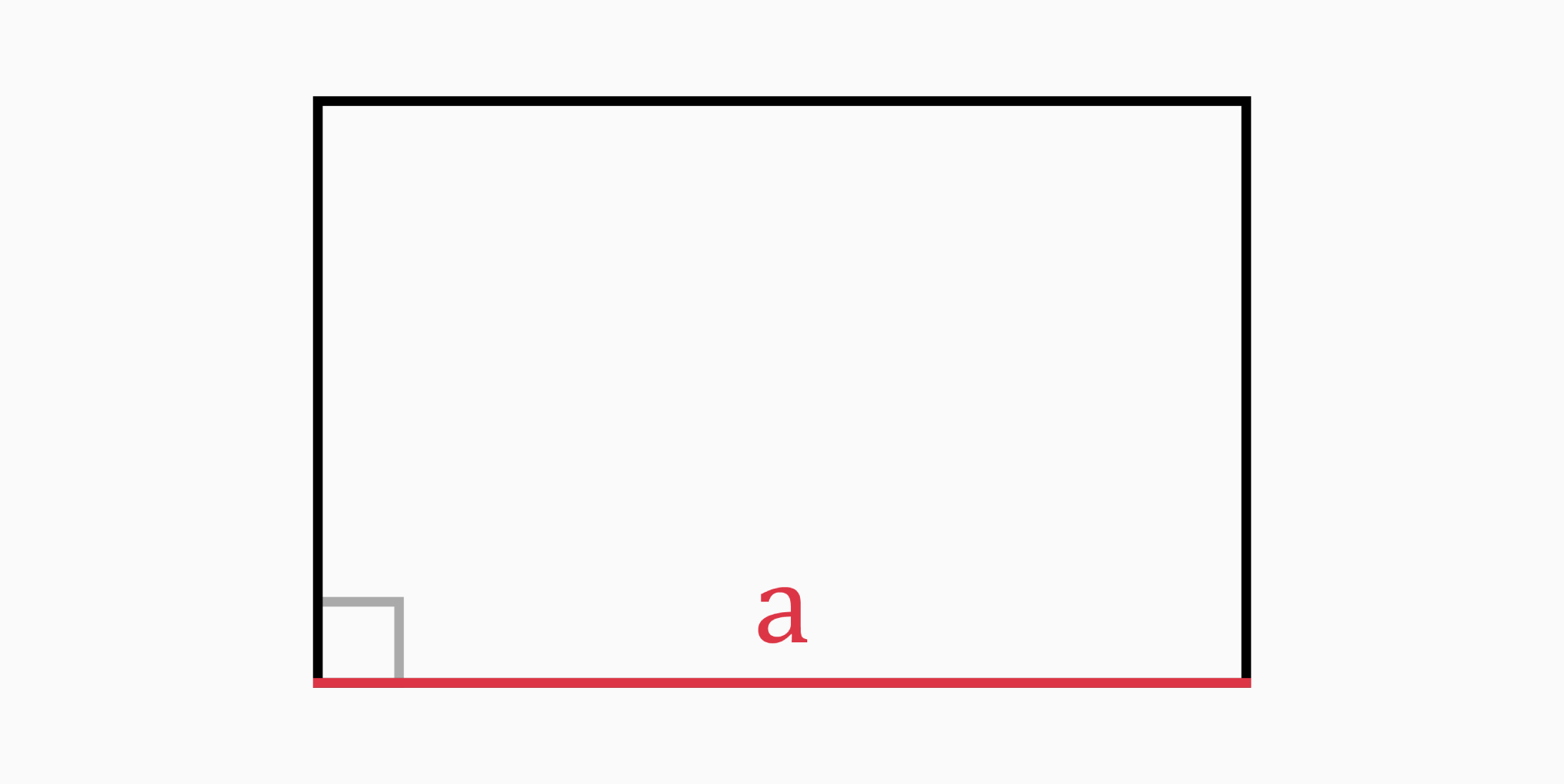
The length of a rectangle is the longer side of the rectangle.

It can be found with the following formulas:

• If you know the width and the perimeter of the rectangle:

  a = (P – 2 * b) / 2

• If you know the width and the area:

  a = A / b

• If you know the width and the diagonal:

  a = √(d² - b²)

Width (b)

The width of a rectangle is the shorter side of the rectangle.

You can determine it with these formulas:

• If you know the length and the perimeter of the rectangle:

  b = (P – 2 * a) / 2

• If you know the length and the area:

  b = A / a

• If you know the length and the diagonal:

  b = √(d² - a²)

Area (A)

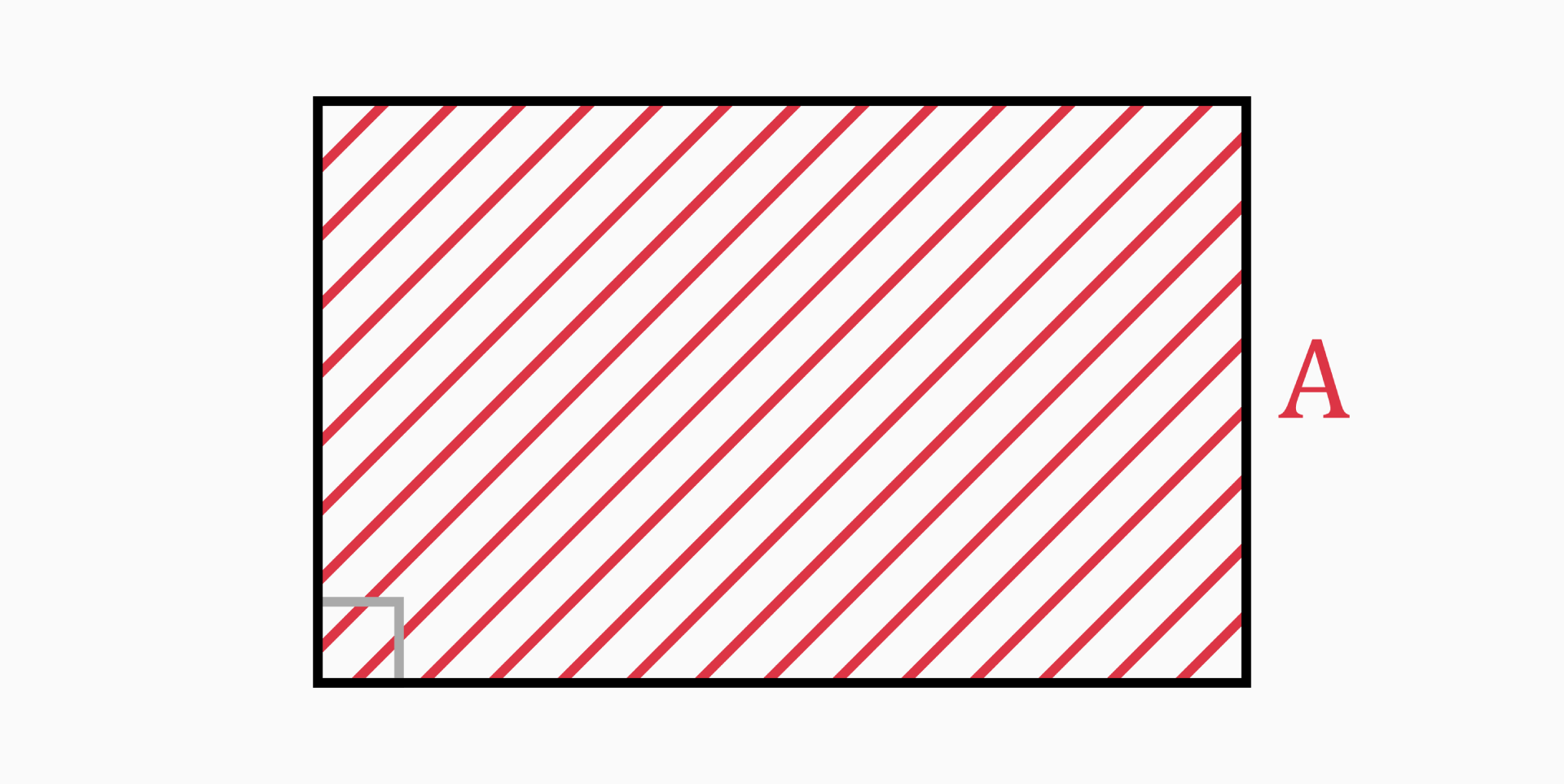
The area of a rectangle is the region enclosed inside the rectangle.

It can be calculated with the following formula:

A = a * b

Perimeter (P)

The perimeter of a rectangle is the distance around the boundary of the rectangle.

You can find it with the following formula:

P = 2 * a + 2 * b = 2 * (a + b)

Diagonal (d)

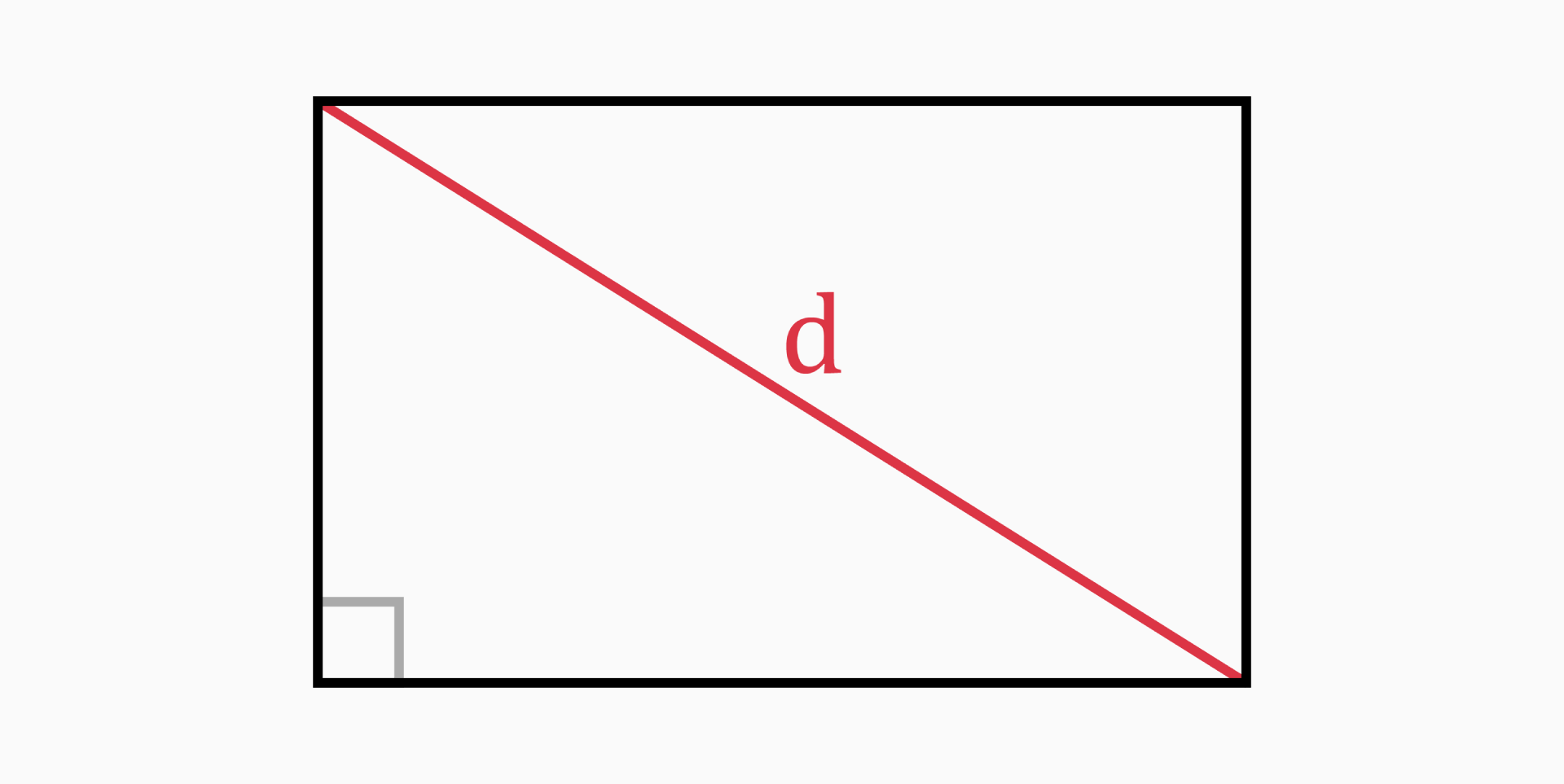
The diagonal is the length of a line stretching from one corner of the rectangle to the opposite corner through the center of the rectangle.

The diagonal of the rectangle cuts the rectangle in two right triangles. The length and width are the side lengths of a triangle; Therefore, we can use the diagonal as the hypotenuse of the triangle.

In this case, the Pythagorean theorem can be applied:

d² = a² + b²

which simplifies to:

d = √(a² + b²)

Circumradius (R)

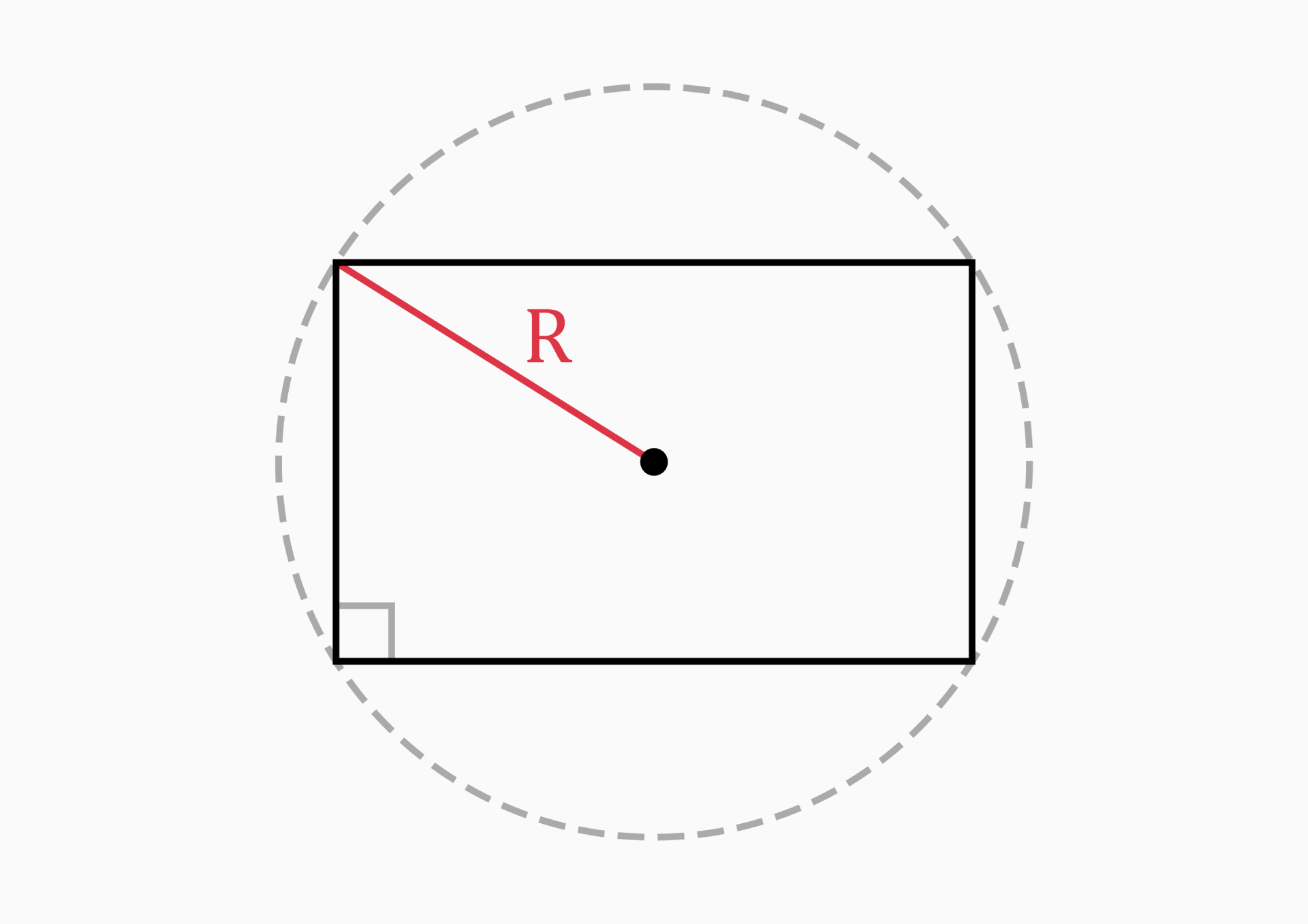
The circumradius is the radius of a circle which is drawn outside a rectangle touching all four vertices (corners) of the rectangle.

From the drawing above, we can clearly understand the circumradius is half of the diagonal of the rectangle.

Therefore, the formula of the diagonal should be divided by 2:

R = d / 2 = √(a² + b²) / 2