Hexagon Calculator

Table of Contents

• Hexagon definition
• Parts of a hexagon
  • Side length (a)
  • Area (A)
  • Perimeter (P)
  • Apothem (r)
  • Circumradius (R)
• Types of hexagons

Hexagon definition

A hexagon is a shape with six sides and six angles.

The most common type of hexagon, and the one that we will talk about below, is the regular hexagon, which is a special type of polygon. This is because all sides of a regular hexagon have the same length and all angles have the same measure.

Hexagons are often found in nature, such as in the shapes of honeycomb cells, and in various fields such as mathematics, architecture, and design.

For regular hexagons, the following properties apply:

• All sides are equal in length.
• All interior angles measure 120°.
• All exterior angles measure 60°.
• It can be divided into six equilateral triangles.
• The opposite sides are parallel to each other.

Parts of a hexagon

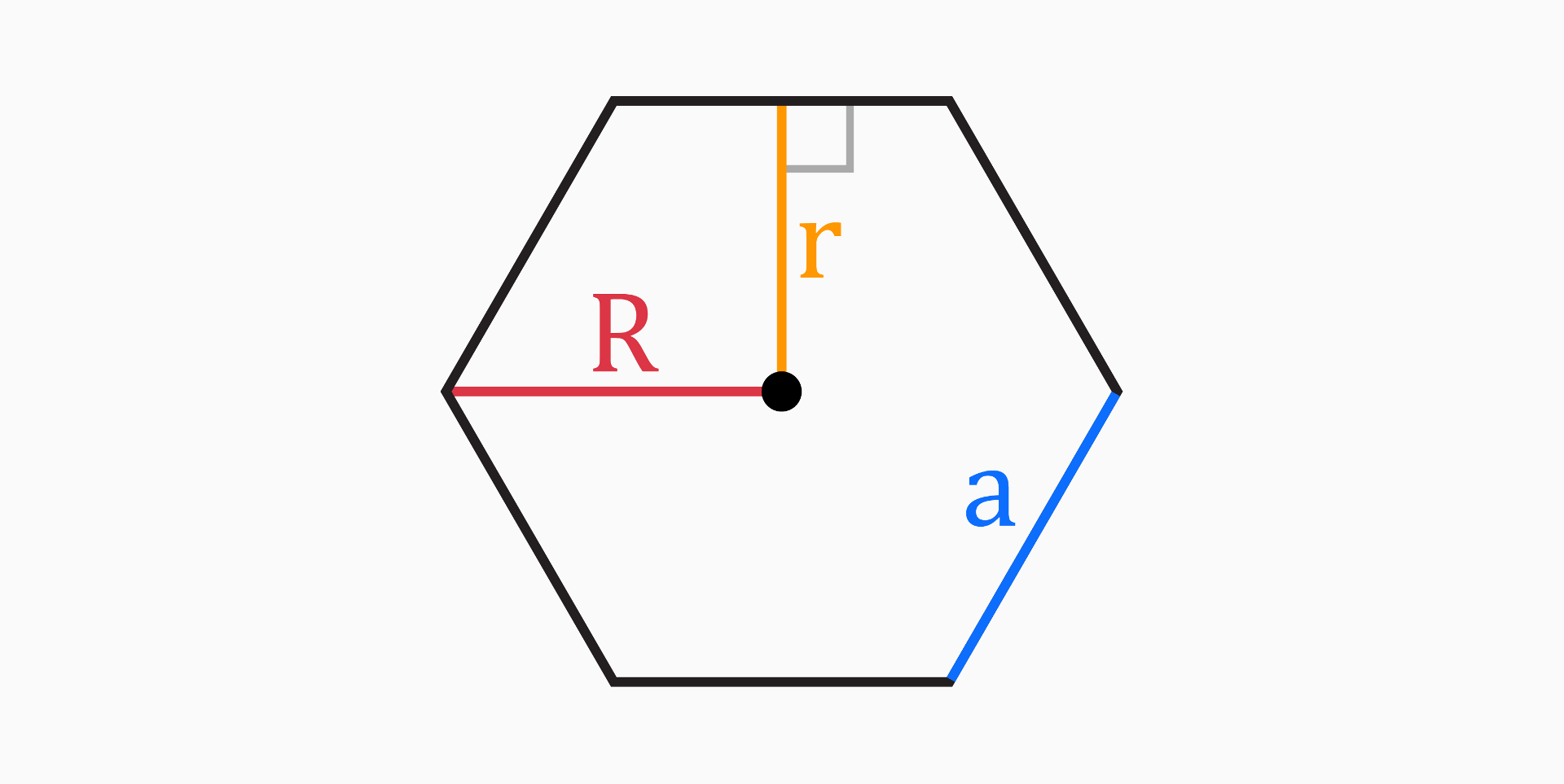
The five parts of a regular hexagon mentioned in this tool are: side length (a), area (A), perimeter (P), apothem (r) and circumradius (R).

Side length (a)

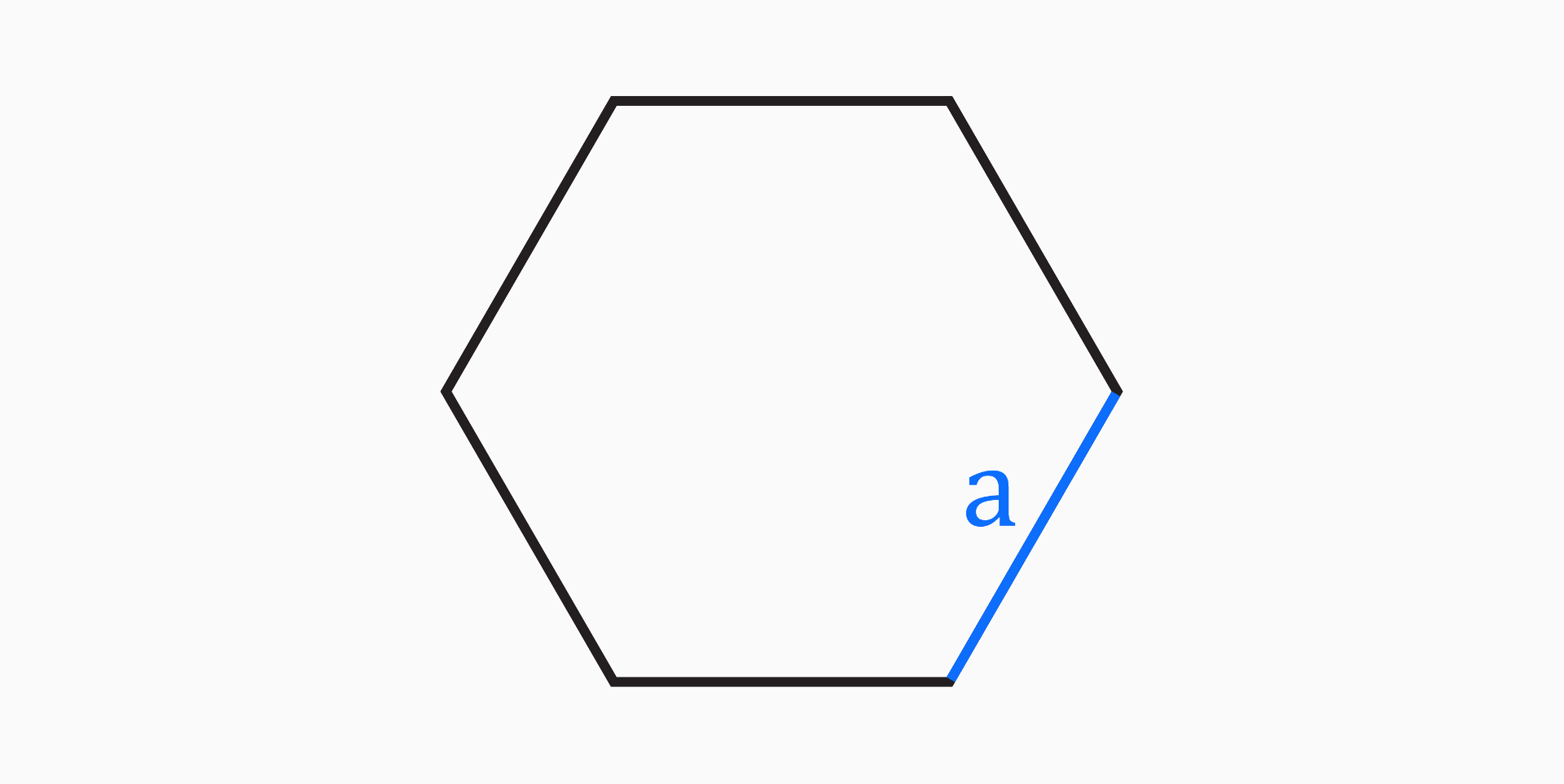
The side length of a regular hexagon is a measure of the distance from one vertex to another along one of the sides.

It can be calculated using the following formulas:

• If you know the perimeter of the hexagon:

  a = P / 6

• If you know the apothem:

  a = 2 * r / √(3)

• If you know the area:

  a = √(2 * A / 3 / √(3))

Area (A)

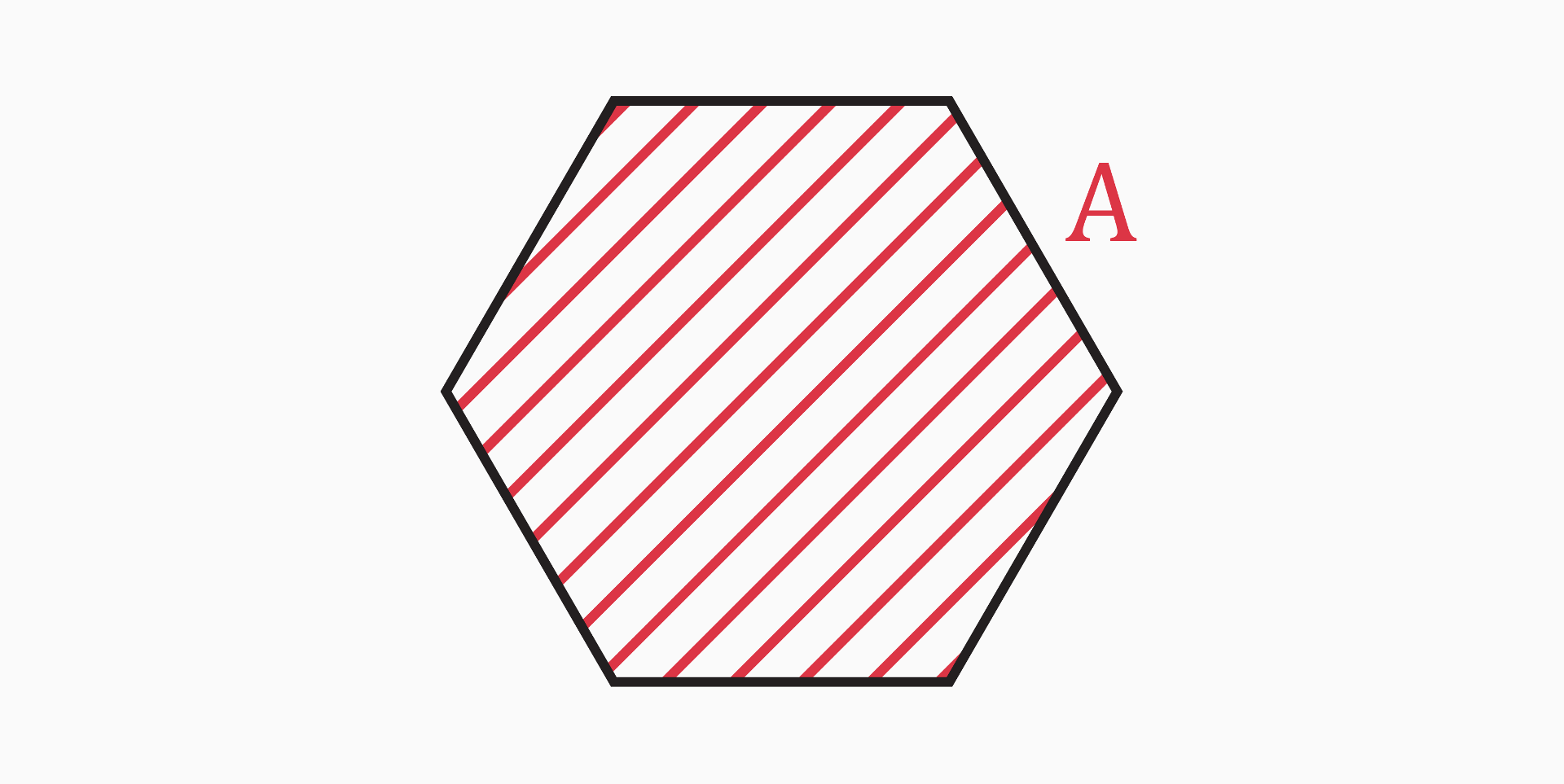
The area of a regular hexagon is a measure of the size of the hexagonal region it encloses.

• The formula for calculating the area of a polygon is always the same, no matter how many sides it has, as long as it is a regular polygon:

  A = r * P / 2

• If you know only the side length of the hexagon, you can still find the area, using the following formula:

  A = 3 * √(3) / 2 * a²

Perimeter (P)

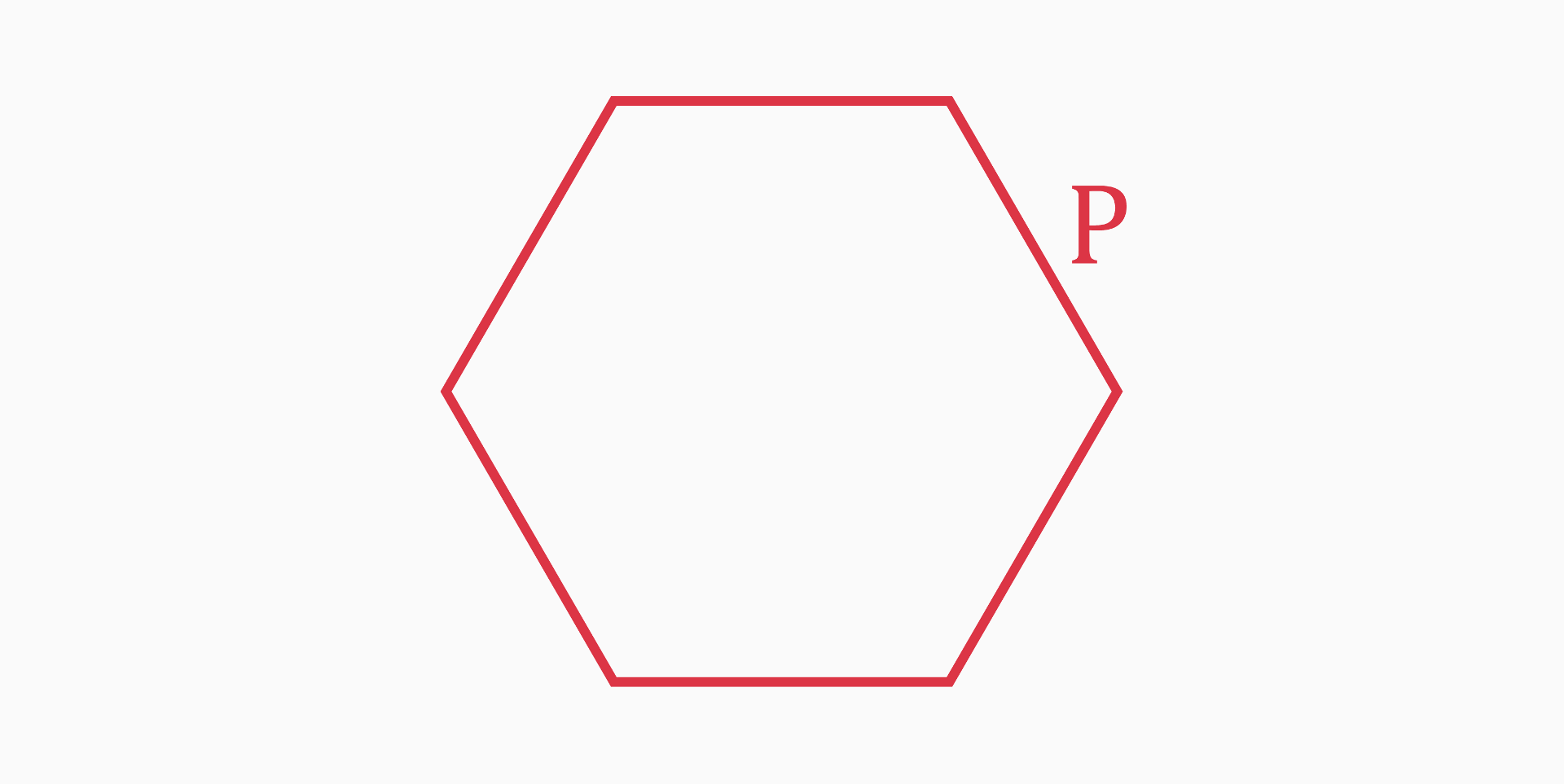
The perimeter of a regular hexagon is a measure of the total distance around the hexagonal shape.

The formula for calculating the perimeter of a regular hexagon is:

P = 6 * a

Apothem (r)

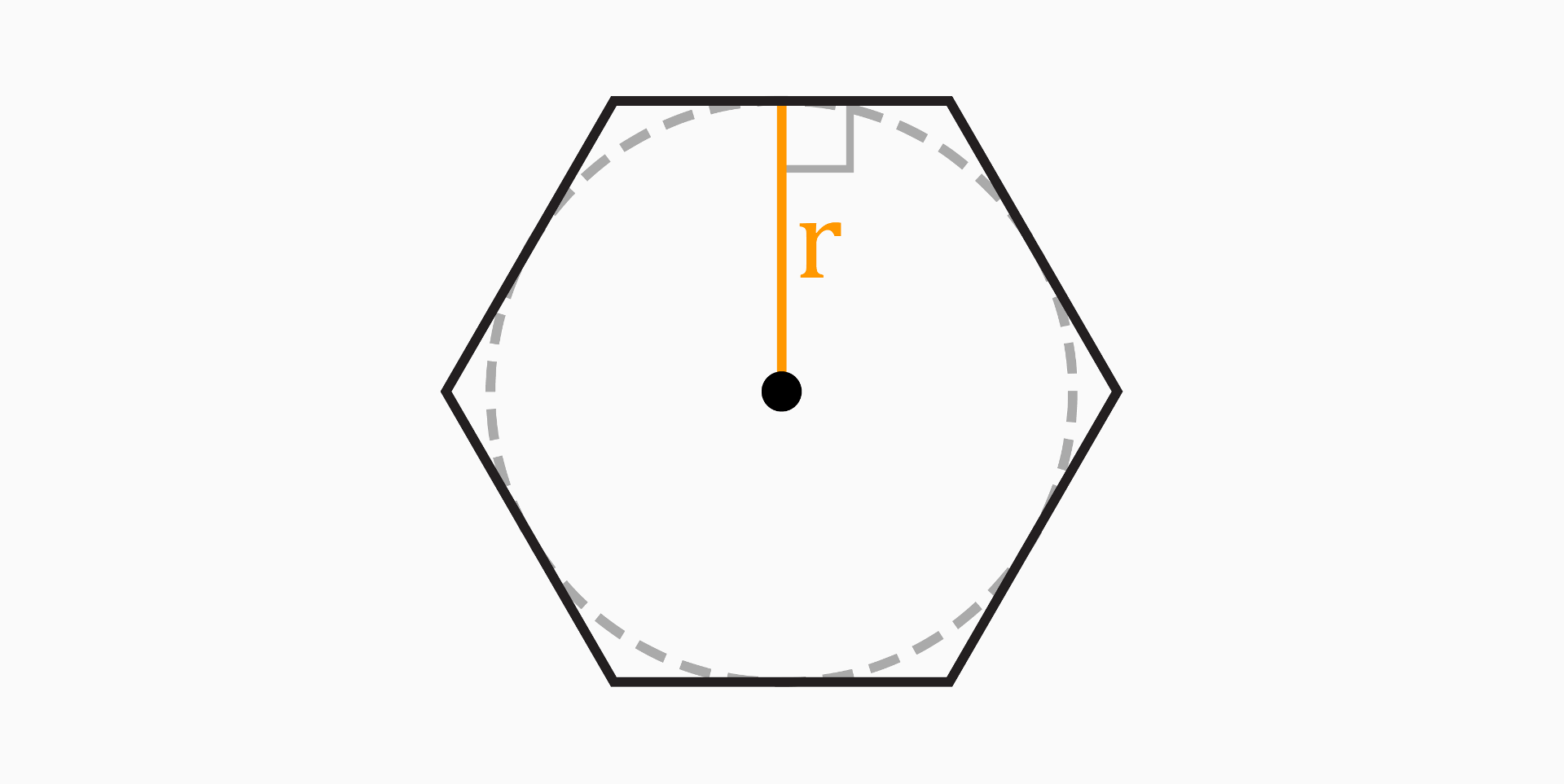
The apothem of a regular hexagon is a line segment that runs from the center of the hexagon to the midpoint of one of its sides.

The formula for calculating the apothem is:

r = a * √(3) / 2

Circumradius (R)

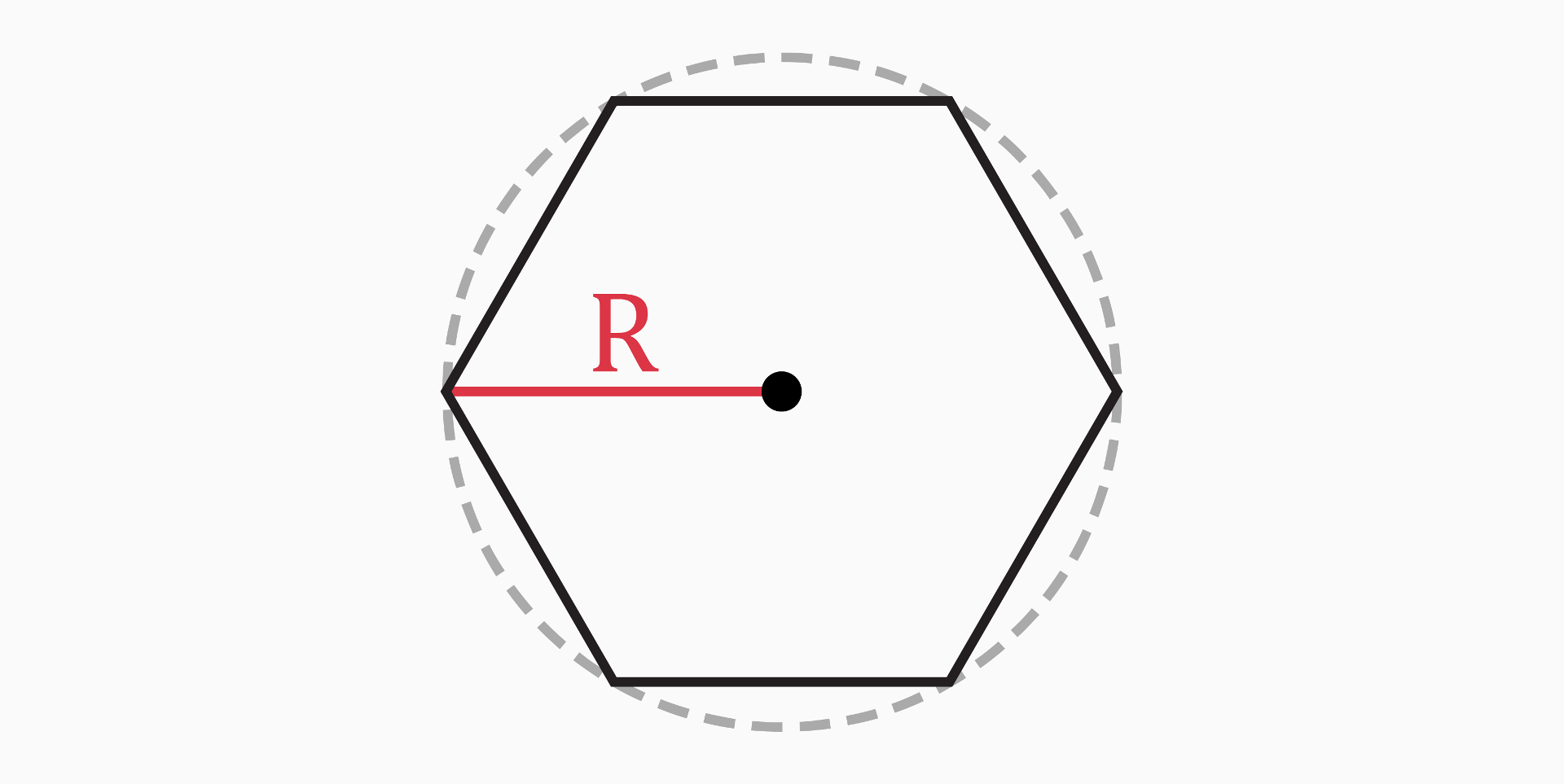
The circumradius of a regular hexagon is the distance from the center of the hexagon to one of its vertices.

In the case of a regular hexagon, it is simply equal to the side length.

R = a

Types of hexagons

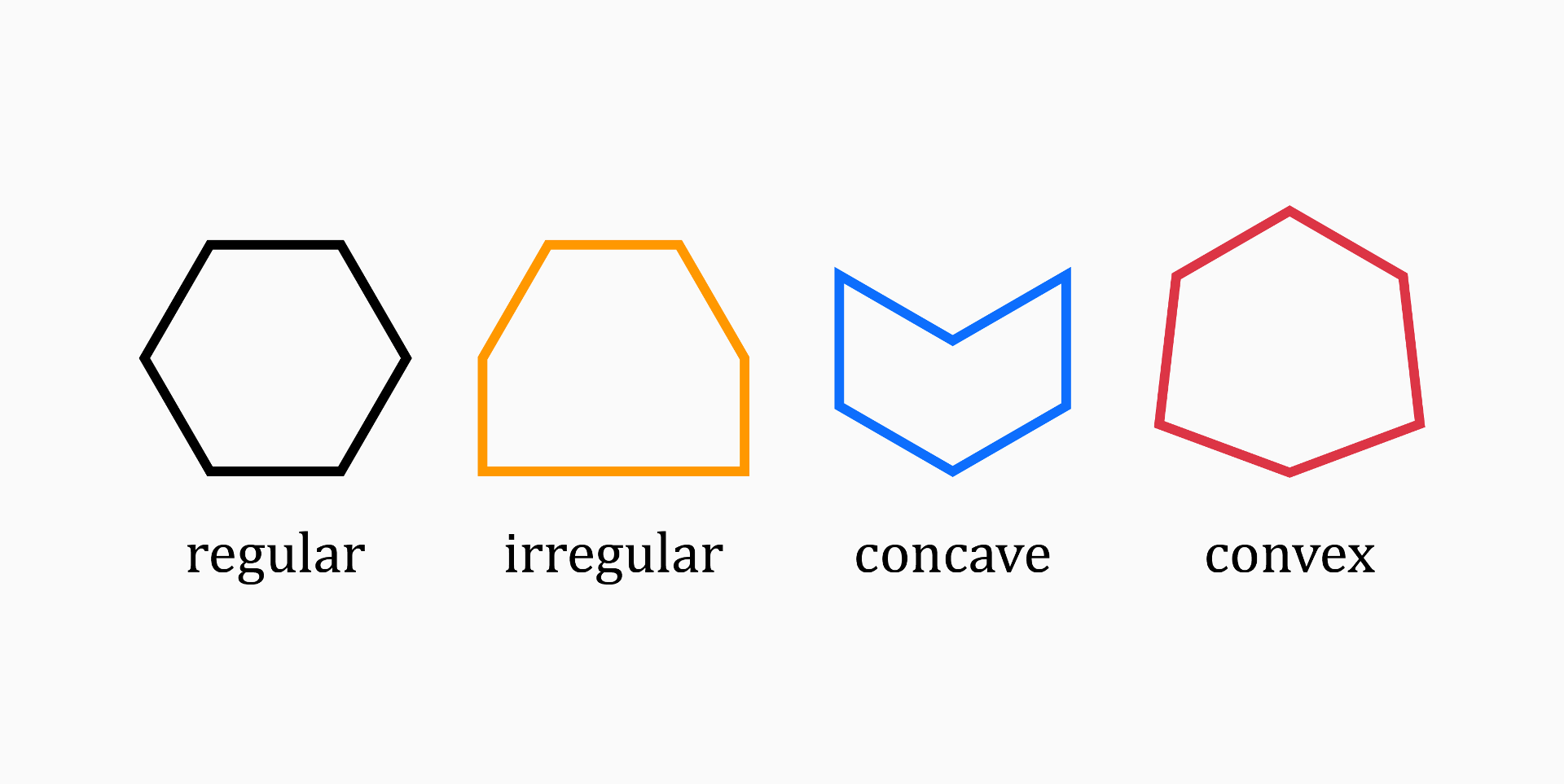
Hexagons can be divided into various categories based on the measurements of their sides and angles.

Based on their sides, they can be classified as:

• Regular hexagons, when the length of all the sides and measure of all the angles are equal.

• Irregular hexagons, when the length of sides and measure of angles do not have the same measure.

Based on their angles, they can be classified as:

• Convex hexagons, when all of the interior angles are less than 180 degrees, and all the vertices are pointed outwards. Convex hexagons can be regular or irregular.

• Concave hexagons, when at least one of the interior angles is greater than 180° and at least one vertex points inwards. Concave hexagons are always irregular.