Circle Calculator

Table of Contents

• Circle definition
• Parts of a circle
  • Radius (r)
  • Diameter (d)
  • Area (A)
  • Circumference (c)
• Unit circle
• Pi (π)

Circle definition

A circle is a round plane figure with no corners or edges. It is a two-dimensional closed curve, made of points that are at equal distance from a given point – the center.

The name circle derives from the Greek κίρκος/κύκλος (kirkos/kuklos), meaning hoop or ring.

Parts of a circle

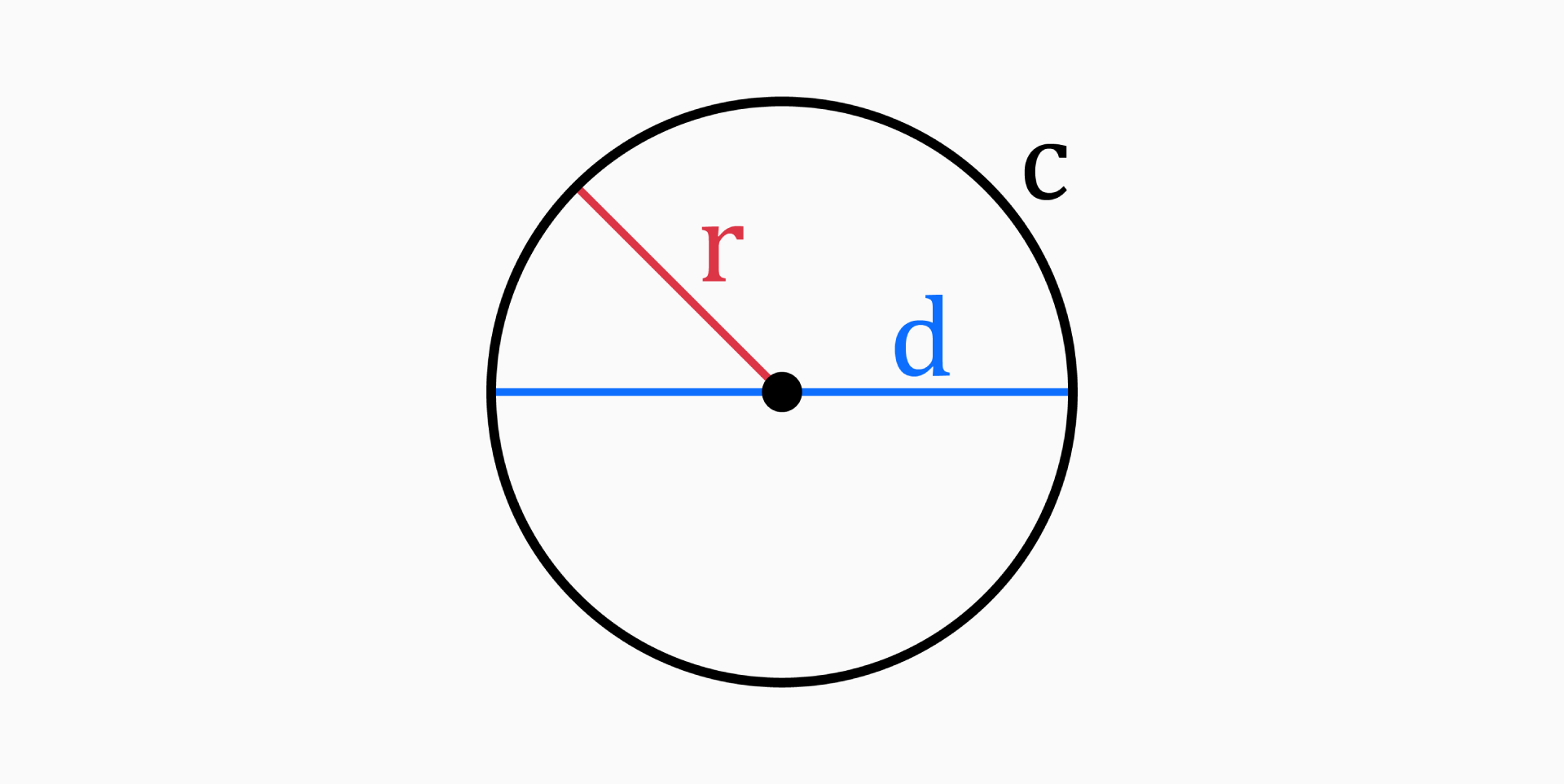
The four main parts of a circle are radius (r), diameter (d), area (A) and circumference (c).

Radius (r)

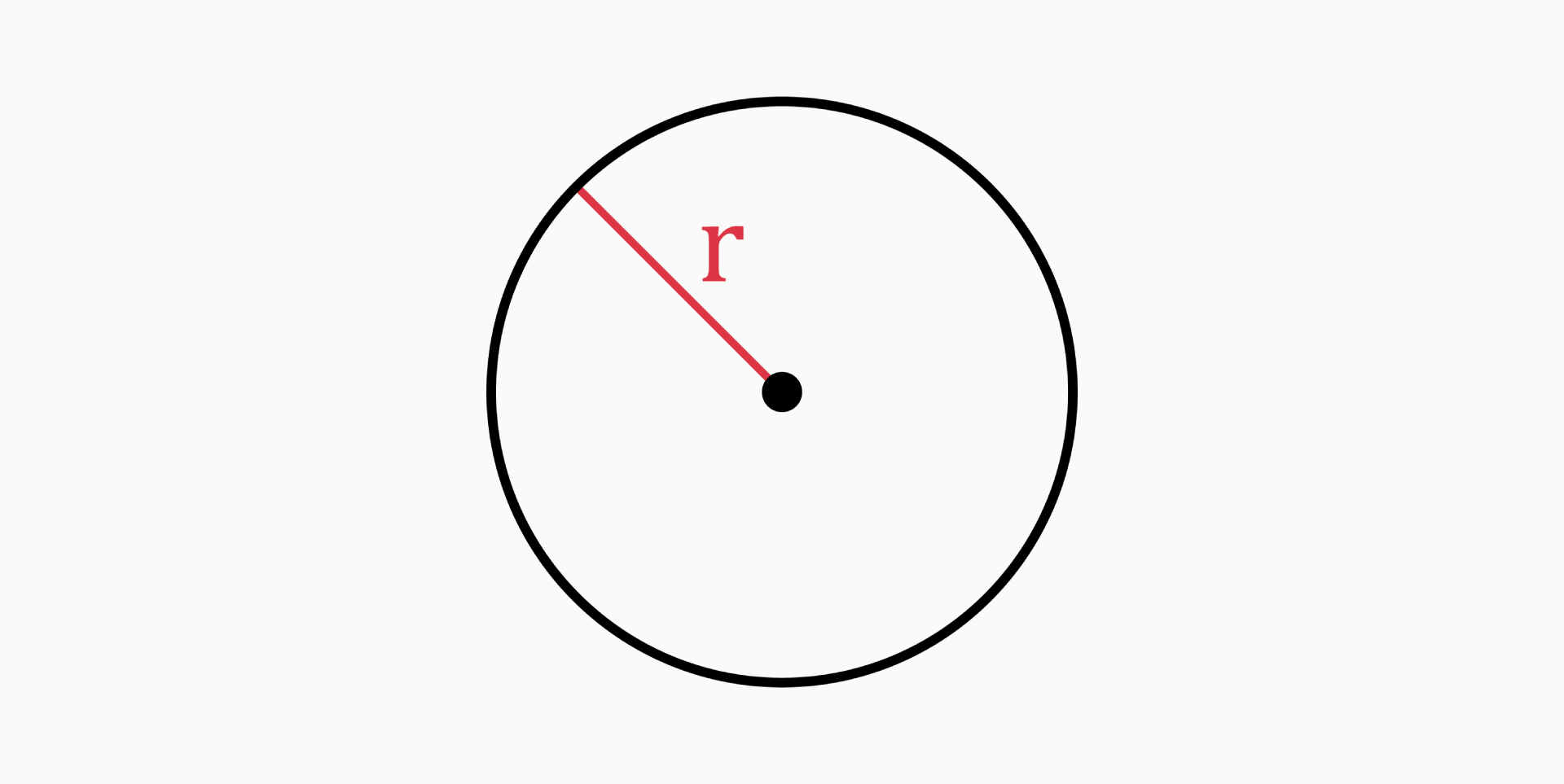
The radius of a circle is the distance from the center of the circle to any point on it's circumference.

It can be found with the following formulas:

• If you know the diameter of the circle:

  r = d / 2

• If you know the circumference:

  r = c / (2 * π)

• If you know the area:

  r = √(A / π)

Diameter (d)

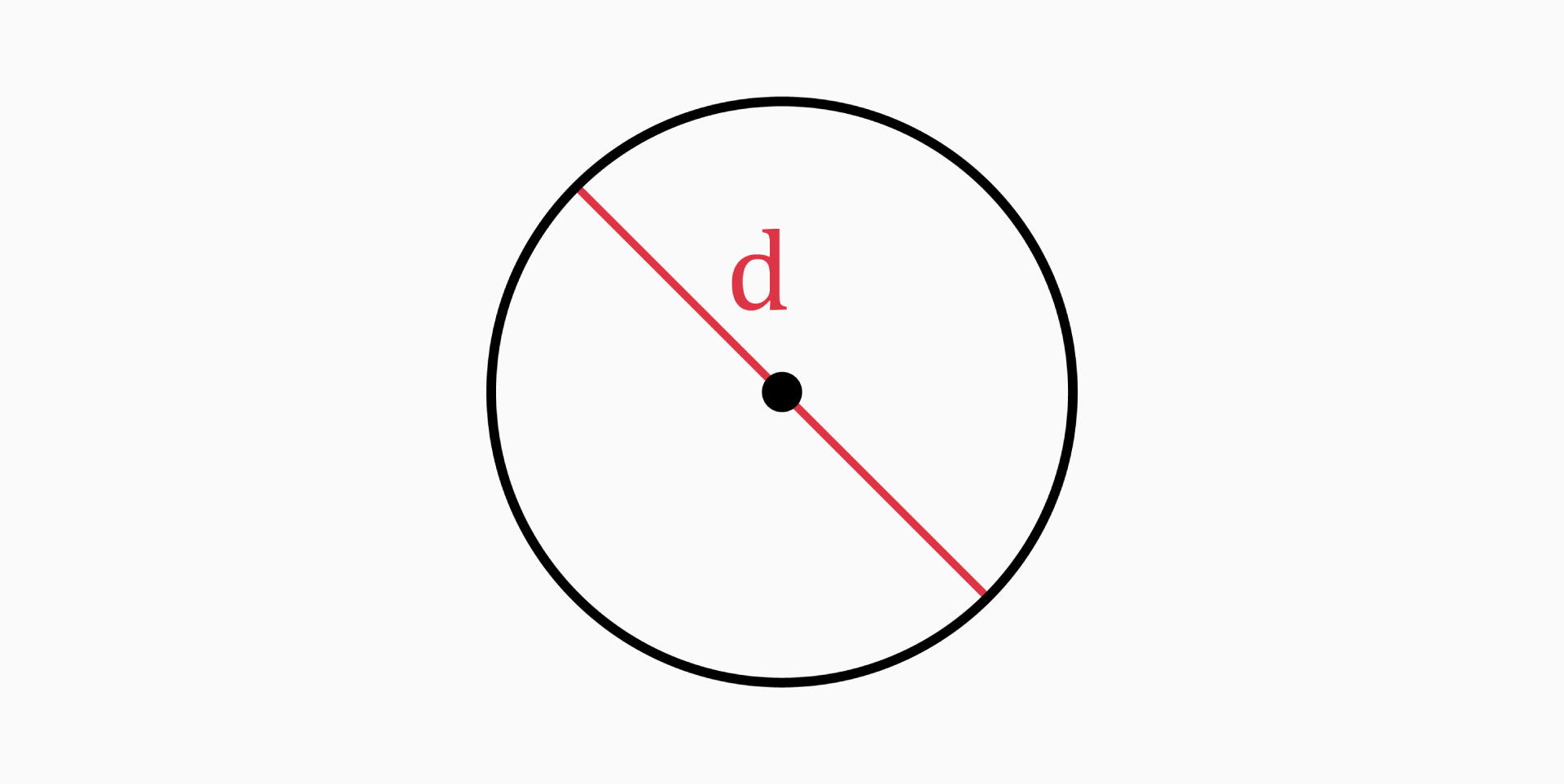
The diameter of a circle is the length of a line that passes through the center and joins two points on the circle.

You can determine it with these formulas:

• If you know the radius of the circle:

  d = 2 * r

• If you know the circumference:

  d = c / π

• If you know the area:

  d = 2 * √(A / π)

Area (A)

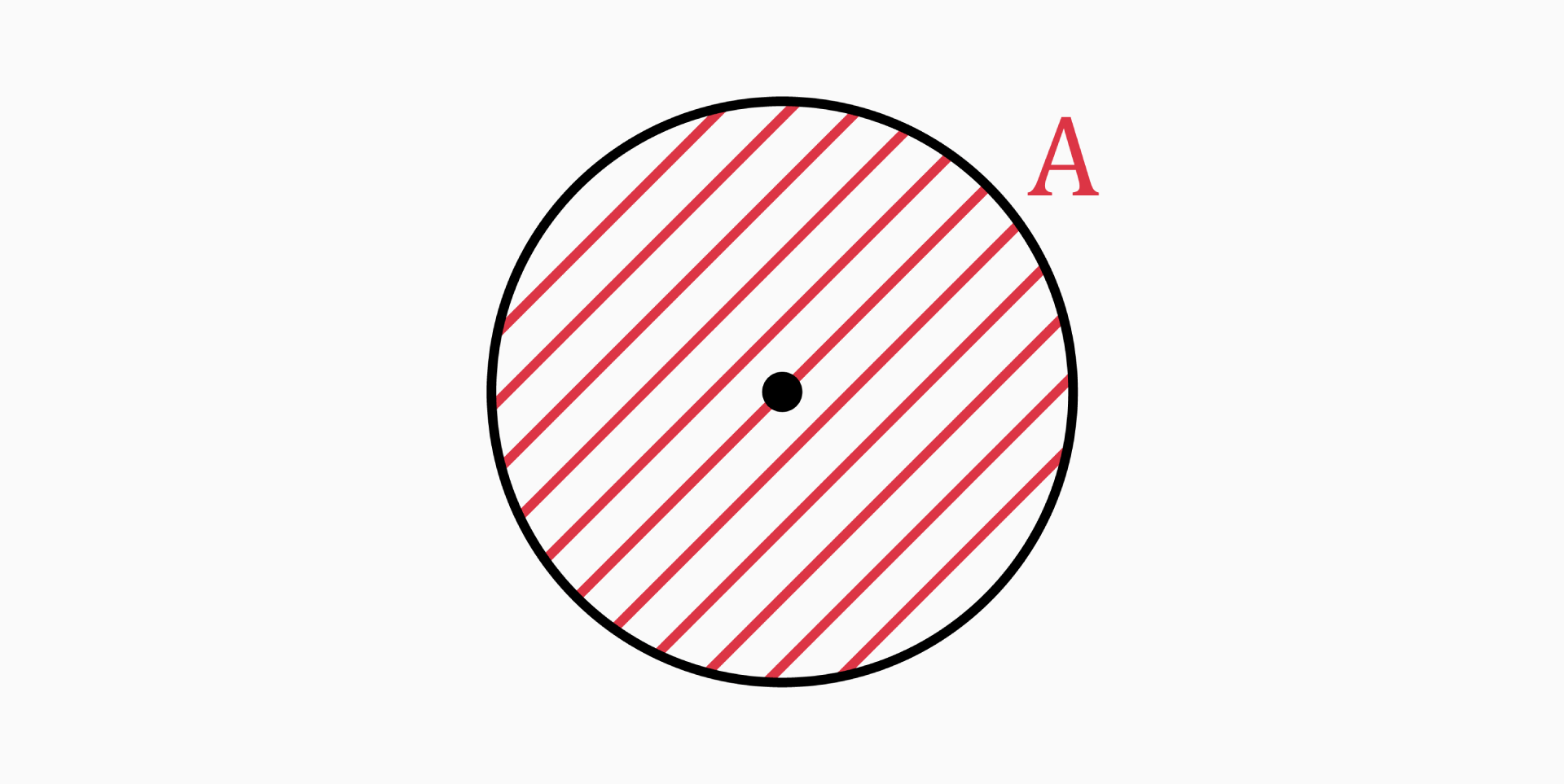
The area of a circle is the region enclosed inside the circle.

You can calculate it as follows:

• If you know the radius or diameter of the circle:

  A = π * r² = π * (d / 2)²

• If you know the circumference:

  A = c² / (4 * π)

Circumference (c)

The circumference of a circle is the distance around the boundary of that circle.

You can calculate it with the following formulas:

• If you know the radius or diameter of the circle:

  c = 2 * π * r = π * d

• If you know the area:

  c = 2 * √(π * A)

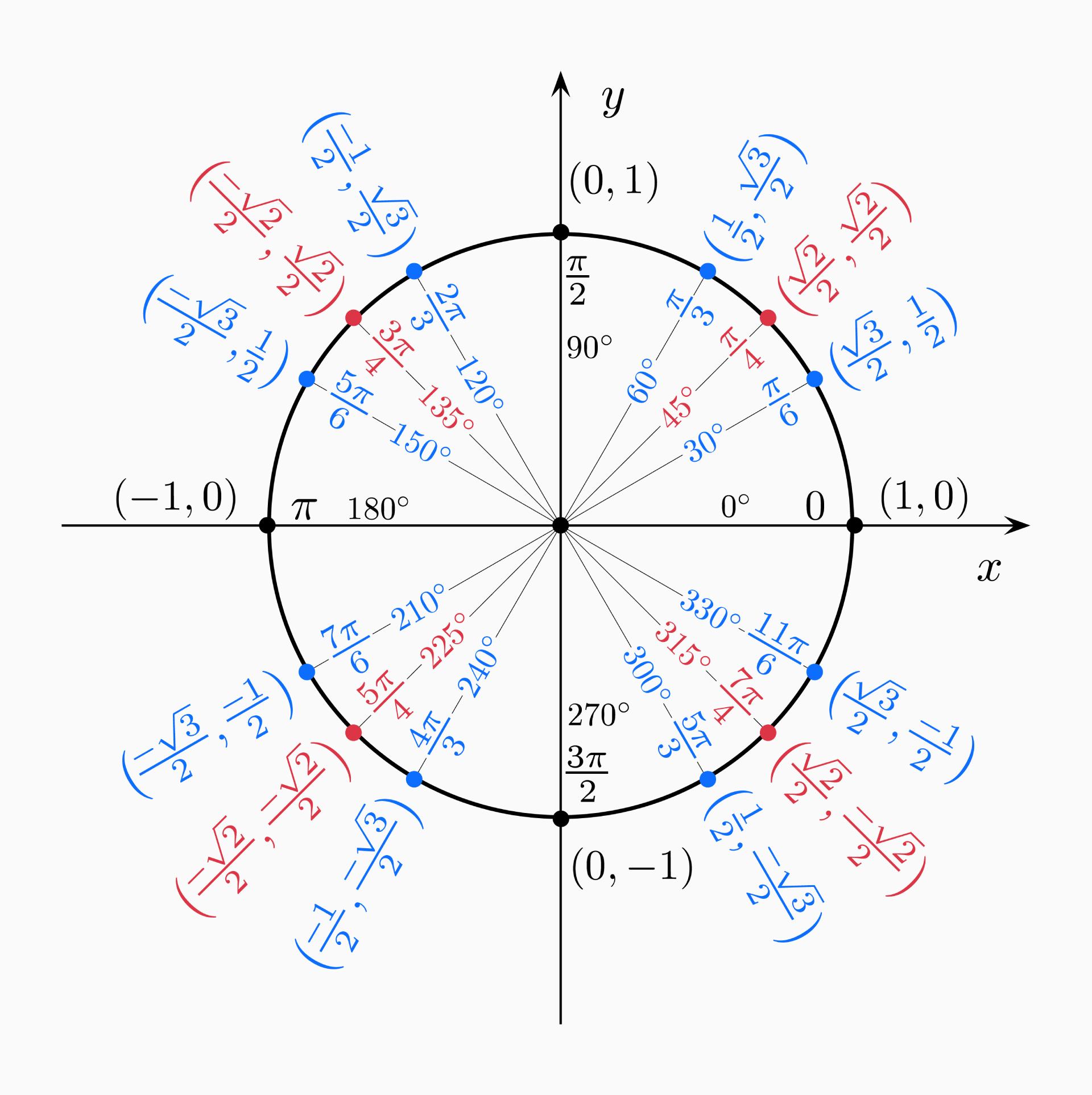
Unit circle

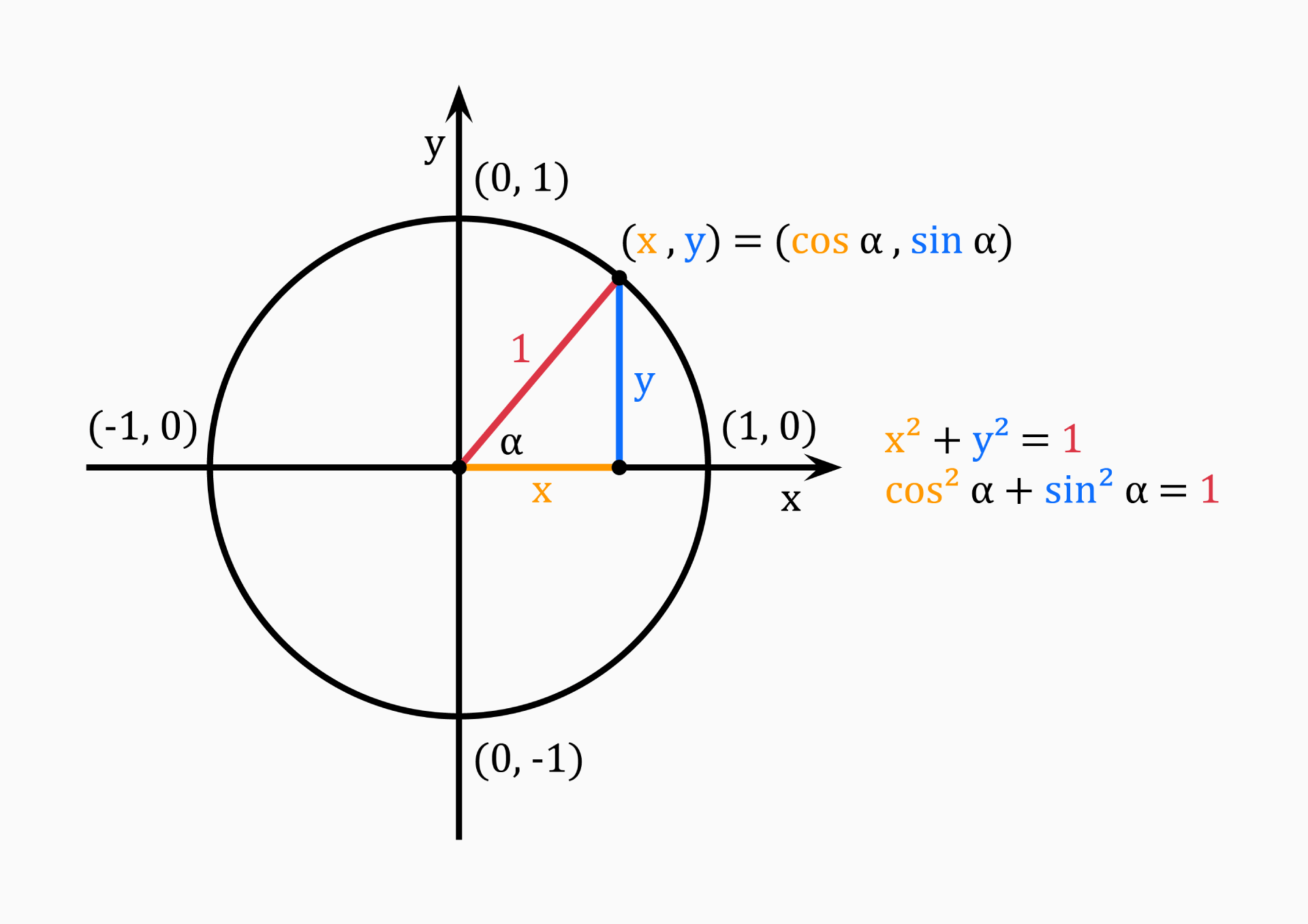
The unit circle is a circle with a radius of 1. Usually, its center is positioned at the origin (0, 0) in the Cartesian coordinate system. The length from the center to any point on the circle is of length 1.

By choosing any point (x, y) on the unit circle, we have x and y as the lengths of the right triangle, with the radius of our circle being the hypotenuse of length 1.

Using the Pythagorean theorem, we can find out that:

x² + y² = 1

This equation works for every quadrant, since:

x² = (-x)²

We can also define the right triangle in terms of sine and cosine:

cos(α) = x / 1 = x

sin(α) = y / 1 = y

which results in:

cos²(α) + sin²(α) = 1

This equation is known as the Pythagorean trigonometric identity.

Pi (π)

The number π is a mathematical constant, defined as the ratio of a circle’s circumference to its diameter. Regardless of the circle’s size, the ratio c / d is constant.

π = circumference / diameter

The number π is an irrational number and its digits never repeat. Pi has been calculated to one hundred trillion digits beyond its decimal point (2022), however this constant is an infinite decimal.

π ≈ 3.14159265358979323846264338327950288419716939937510…