Power Triangle Calculator
Table of Contents
Active, reactive, and apparent power
If you want to understand the power triangle, you first need to understand each of its three components: active power (P), reactive power (Q), and apparent power (S).
Active power (P)
Active power (also called real power) is the power that is actually consumed by the load and is responsible for performing useful work. It is measured in watt (W) and is represented by the letter P in the power triangle.
Active power is the only form of power in a DC circuit. In an AC circuit, there are no fixed current and voltage values; they change sinusoidally. If there is no phase shift between these two values, then all of the power transferred is active power.
Reactive power (Q)
Reactive power is the power that is stored in and returned by the load, and is not used to perform useful work. It is measured in volt-ampere reactive (VAR) and is represented by the letter Q in the power triangle.
This is the electric power that flows to and from an AC circuit due to capacitors and inductors receiving it in one half and returning it (to the power supply) in the next half of the cycle.
Apparent power (S)
Because of the different reactive components (capacitors and inductors) in an AC circuit, the current and voltage waveforms are not in-phase.
Due to this phenomenon, there is a mathematical relationship between the active power (P), and the reactive power (Q), called the complex power.
The complex power is the product of the RMS (root mean square) voltage applied to an AC circuit, and the RMS current flowing into that circuit. This power is known generally as apparent power. It is measured in volt-ampere (VA) and is represented by the letter S in the power triangle.
This complex power is not equal to the algebraic sum of the active and reactive power added together, but is instead the vector sum of P and Q, and represents the total power consumed by an AC circuit.
Power triangle of an AC circuit
The power triangle, as a fundamental concept in electrical engineering, is a graphical representation of the relationship between the three key electrical quantities in an AC power system, explained above.
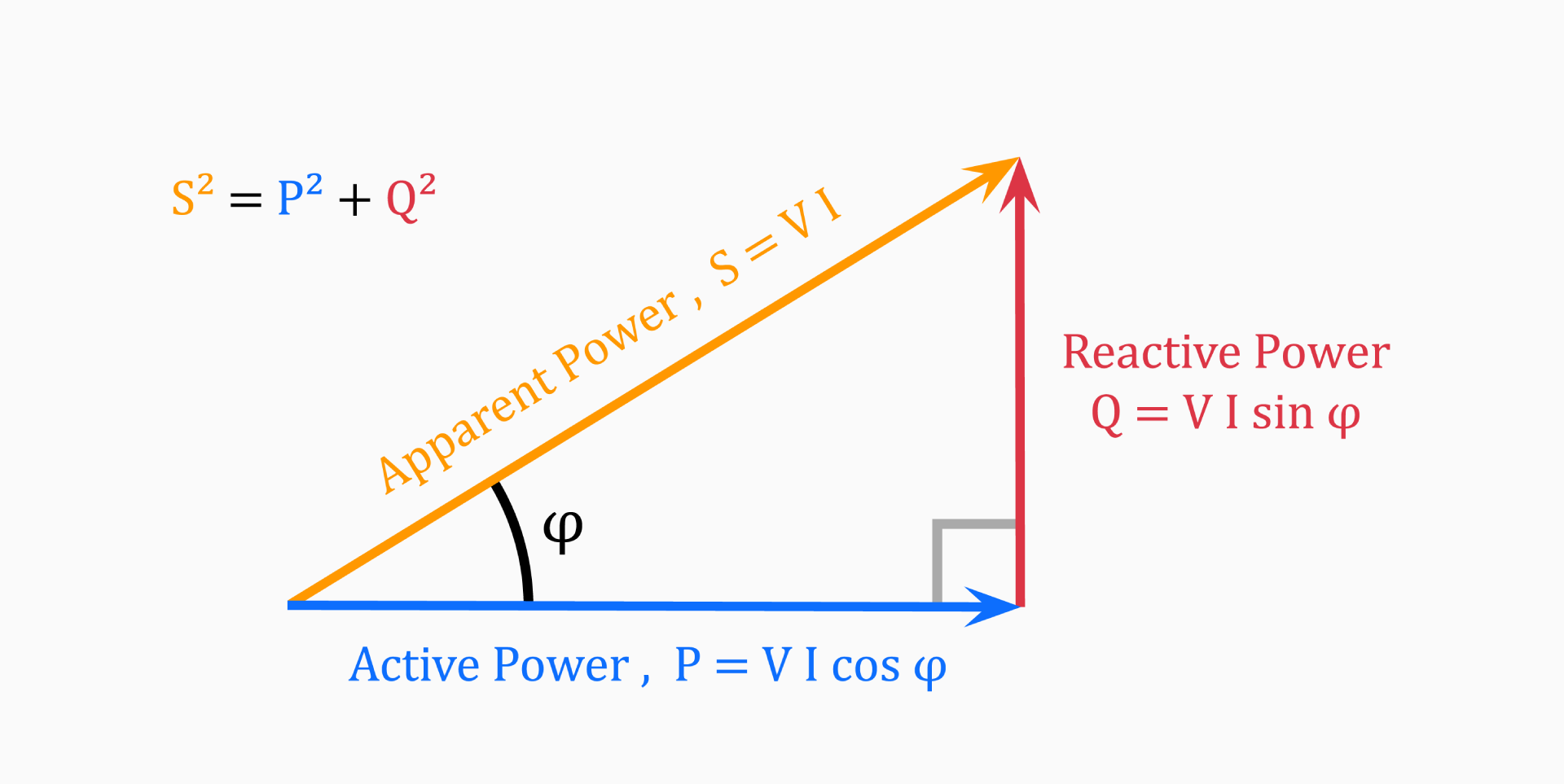
The horizontal (adjacent) side represents the circuits active power (P), the vertical (opposite) side represents the circuits reactive power (Q) and the hypotenuse represents the resulting apparent power (S), of the power triangle as shown above.
One of the consequences of using the power triangle is that we can easily establish the mathematical relationship between the three values with the use of the Pythagorean theorem:
S² = P² + Q²
From this we can derive the following equations:
-
Active power
P = √(S² - Q²) -
Reactive power
Q = √(S² - P²) -
Apparent power
S = √(P² + Q²)
Power factor of an AC circuit
There is a fourth component in the power triangle; the angle between the active and apparent power, denoted with φ (phi), is the circuit's phase angle. The cosine of this angle φ, cos(φ), is the power factor of the circuit.
Power factor is an important part of an AC circuit that is defined as the ratio of active power (P) to apparent power (S), and is generally expressed as either a decimal value, for example 0.85, or as a percentage: 85%.
power factor = P / S = cos(φ)
If you know the power factor cos(φ), and either P or S, you can easily calculate the other one:
P = S * cos(φ)
S = P / cos(φ)
It is always desirable to have a high power factor as this makes the most efficient use of the circuit delivering current to a load.
For example, a power factor of 0.85 means that 85% of the current you supply to the circuit is performing real work. The rest of the power - 15%, to be exact - has to be provided to make up for the reactive power. Knowing how to calculate the power factor is useful in computations regarding power generators, uninterruptible power supplies and more.
