Angle Converter
Table of Contents
Angle definition
An angle is a unit of measurement that describes the amount of rotation between two intersecting lines or planes. In mathematics, angles are used to describe the orientation of objects in two-dimensional or three-dimensional space. Angles are represented by symbols, such as the Greek letters alpha (α), beta (β), theta (θ), and are typically measured in units of degrees, radians, or gradians.
Types of angles
Angles are defined by their size, which is the amount of rotation between the lines or planes that form the angle, and their direction, which is determined by the order in which the lines or planes are rotated.
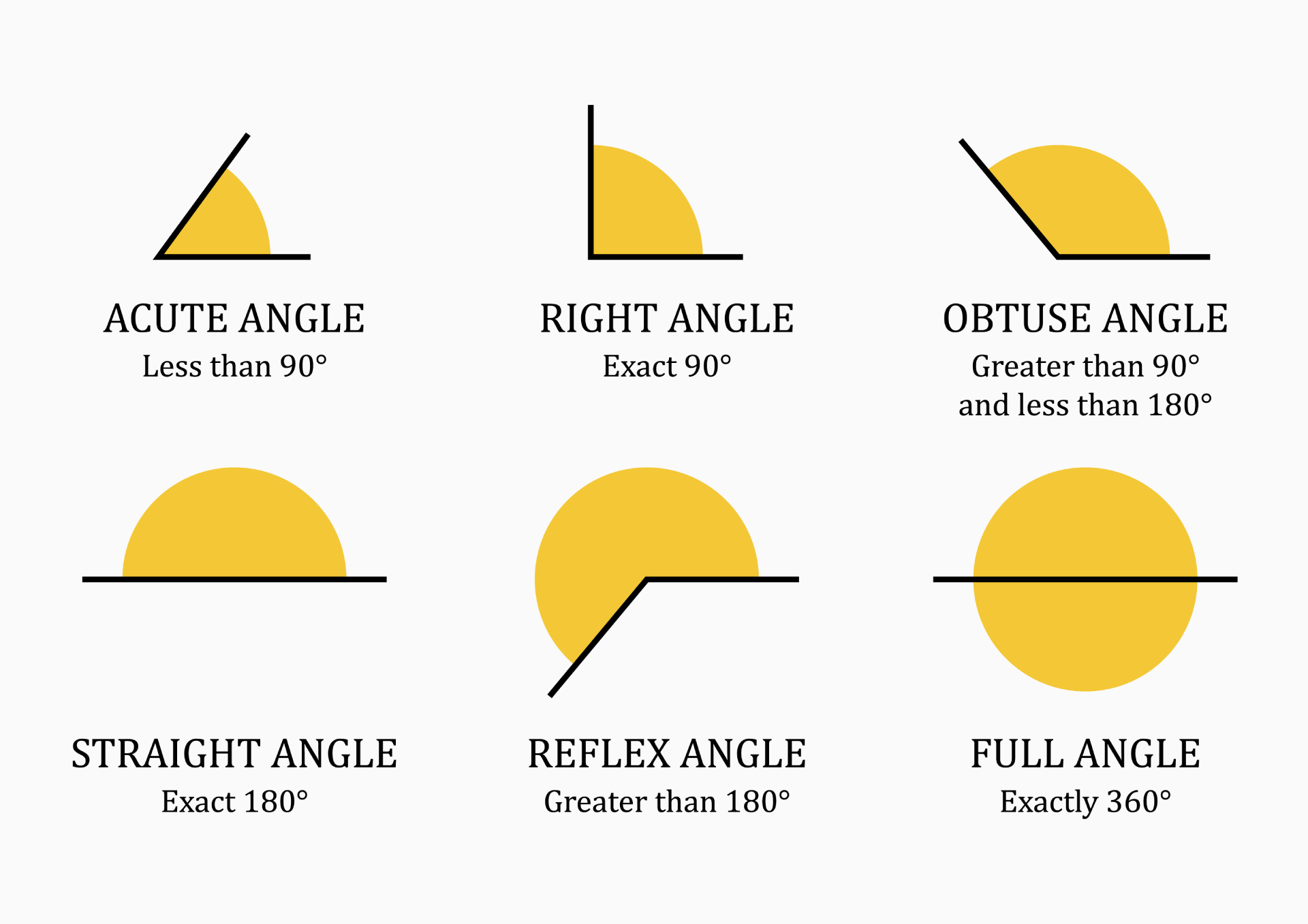
There are six main types of angles: acute, right, obtuse, straight, reflex and full angles.
-
Acute angles - An acute angle is an angle with a measure less than 90 degrees. It is an angle that is smaller than a right angle.
-
Right angles - A right angle is an angle with a measure of exactly 90 degrees. It is an angle that forms a square corner.
-
Obtuse angles - An obtuse angle is an angle with a measure greater than 90 degrees but less than 180 degrees. It is an angle that is greater than a right angle but smaller than a straight angle.
-
Straight angles - A straight angle is an angle with a measure of exactly 180 degrees. It is an angle that forms a straight line.
-
Reflex angles - A reflex angle is an angle with a measure greater than 180 degrees. It is an angle that is greater than a straight angle, but smaller than a full circle.
-
Full angles: A full angle, also known as a complete angle, full rotation or a perigon, is an angle with a measure of 360 degrees. It is an angle that completes a full circle.
Angles can also be described as positive or negative, depending on the direction of rotation. In mathematics, positive angles are defined as angles that rotate in a counterclockwise direction, while negative angles are defined as angles that rotate in a clockwise direction.
Angle units
Below, we will discuss some of the most commonly used angle units and the conversion factors between them.
Radians
The radian is the unit of angle in the International System of Units (SI). It is based on the relationship between an angle and its corresponding arc length on a unit circle.
It is defined as the angle subtended by an arc of length equal to the radius of the circle.
One full circle is equal to 2π radians, and one radian is 180°/π, or about 57.2958 degrees.
Degrees
The degree is a unit of angular measurement usually denoted by ° (the degree symbol).
It is defined as 1/360 of a full circle, so one full circle is 360 degrees.
The degree is not an SI unit, but it is mentioned in the SI brochure as an accepted unit.
Minutes and Seconds
Minutes and seconds are also units of angular measurement, usually denoted by ' and ", that are used in conjunction with degrees to describe angles in the DMS format.
One minute is equal to 1/60 of a degree, and one second is equal to 1/60 of a minute.
Gradians
The gradian (or gon) is a unit of measurement of angles that is principally used in surveying and mapping application (especially in Europe), and to a lesser extent in mining and geology.
It is defined as 1/400 of a full circle, so one full circle is 400 gradians.
The gradian is not part of the International System of Units (SI).
DMS
The DMS (degrees-minutes-seconds) is a system of angular measurement that divides a full circle into 360 equal parts. Each part is then further divided into 60 minutes, and each minute is divided into 60 seconds.
It is basically a combination of the three units, degrees-minutes-seconds.
The DMS format is represented as a three-part number, for example, 45° 30' 15". In this format, 45 represents the degrees, 30 represents the minutes, and 15 represents the seconds.
The DMS field in CalcKit displays these units together, separated by decimal point, with the first two decimals being the minutes and the next two decimals being the seconds part. For example: 45° 30' 15" can be written as 45.3015 dms.
Converting between units
To convert between the different units of angular measurement, it is important to have a good understanding of the relationships between them. Here are some of the most common conversions:
-
From degrees to radians:
radians = degrees * π / 180 -
From radians to degrees:
degrees = radians * 180 / π -
From degrees to gradians:
gradians = degrees * 400 / 360 -
From gradians to degrees:
degrees = gradians * 360 / 400
